题目内容
14. 如图?ABCD中,AC平分∠DAB,AB=5cm,AC=8cm,则?ABCD的周长为20cm,面积为24cm2.
如图?ABCD中,AC平分∠DAB,AB=5cm,AC=8cm,则?ABCD的周长为20cm,面积为24cm2.
分析 由?ABCD中,AC平分∠DAB,可证得?ABCD是菱形,继而求得答案.
解答  解:连接BD,交AC于点O,
解:连接BD,交AC于点O,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠BAC=∠ACD,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠DAC=∠ACD,
∴AD=CD,
∴?ABCD是菱形,
∴AC⊥BD,OA=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4(cm),
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3(cm),
∴BD=2OB=6cm,
∴?ABCD的周长为4×5=20cm,面积为:$\frac{1}{2}$AC•BD=$\frac{1}{2}$×6×8=24(cm2).
故答案为:20cm,24cm2.
点评 此题考查了平行四边形的性质以及菱形的判定与性质.注意证得?ABCD是菱形是解此题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
4. 如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B的度数是( )
如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B的度数是( )
 如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B的度数是( )
如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B的度数是( )| A. | 80° | B. | 100° | C. | 90° | D. | 95° |
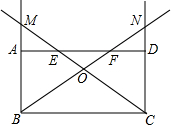 如图,矩形ABCD中,AD=8,AB=4,点E从点A出发,沿A→D方向在线段AD上运动,点F从点D出发,沿D→A方向在线段DA上运动,点E、F速度都是每秒2个长度单位,E、F两点同时出发,且当E点运动到D点时两点都停止运动,设运动时间是t(秒).射线CE交射线BA于点M,射线BF交射线CD于点N,射线BF、CE相交于点O.
如图,矩形ABCD中,AD=8,AB=4,点E从点A出发,沿A→D方向在线段AD上运动,点F从点D出发,沿D→A方向在线段DA上运动,点E、F速度都是每秒2个长度单位,E、F两点同时出发,且当E点运动到D点时两点都停止运动,设运动时间是t(秒).射线CE交射线BA于点M,射线BF交射线CD于点N,射线BF、CE相交于点O.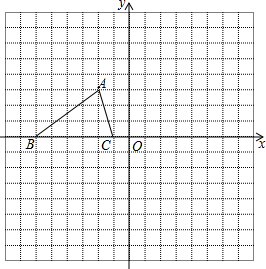 如图,已知△ABC的三个顶点坐标为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC的三个顶点坐标为A(-2,3)、B(-6,0)、C(-1,0). 已知:如图,点D、E分别在AAB、AC上,点F在BC的延长线上,∠A=35°,∠ACF=105°,DE∥BF.求∠ADE的度数.
已知:如图,点D、E分别在AAB、AC上,点F在BC的延长线上,∠A=35°,∠ACF=105°,DE∥BF.求∠ADE的度数.