题目内容
17.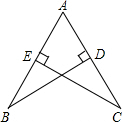 如图,已知AB=AC,BD⊥AC,CE⊥AB,垂足分别为点D,E,说明△ABD与△ACE全等的理由.
如图,已知AB=AC,BD⊥AC,CE⊥AB,垂足分别为点D,E,说明△ABD与△ACE全等的理由.
分析 根据垂直定义得出∠ADB=∠AEC=90°,根据全等三角形的判定定理AAS推出即可.
解答 解:∵BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
在△ABD和△ACE中
$\left\{\begin{array}{l}{∠ADB=∠AEC}\\{∠A=∠A}\\{AB=AC}\end{array}\right.$
∴△ABD≌△ACE(AAS).
点评 本题考查了全等三角形的判定定理的应用,能熟记全等三角形的判定定理的内容是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
8. 如图,点E是等腰三角形△ABD底边上的中点,点C是AE延长线上任一点,连接BC、DC,则下列结论中:
如图,点E是等腰三角形△ABD底边上的中点,点C是AE延长线上任一点,连接BC、DC,则下列结论中:
①BC=AD;②AC平分∠BCD;③AC=AB;④∠ABC=∠ADC.
一定成立的是( )
 如图,点E是等腰三角形△ABD底边上的中点,点C是AE延长线上任一点,连接BC、DC,则下列结论中:
如图,点E是等腰三角形△ABD底边上的中点,点C是AE延长线上任一点,连接BC、DC,则下列结论中:①BC=AD;②AC平分∠BCD;③AC=AB;④∠ABC=∠ADC.
一定成立的是( )
| A. | ①③ | B. | ②③ | C. | ②④ | D. | ①② |
12.若$\frac{3}{4}$x2m+ny与x5ym-n是同类项,则m,n的值是( )
| A. | m=2、n=3 | B. | m=2、n=1 | C. | m=2、n=0 | D. | m=1、n=2 |
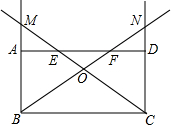 如图,矩形ABCD中,AD=8,AB=4,点E从点A出发,沿A→D方向在线段AD上运动,点F从点D出发,沿D→A方向在线段DA上运动,点E、F速度都是每秒2个长度单位,E、F两点同时出发,且当E点运动到D点时两点都停止运动,设运动时间是t(秒).射线CE交射线BA于点M,射线BF交射线CD于点N,射线BF、CE相交于点O.
如图,矩形ABCD中,AD=8,AB=4,点E从点A出发,沿A→D方向在线段AD上运动,点F从点D出发,沿D→A方向在线段DA上运动,点E、F速度都是每秒2个长度单位,E、F两点同时出发,且当E点运动到D点时两点都停止运动,设运动时间是t(秒).射线CE交射线BA于点M,射线BF交射线CD于点N,射线BF、CE相交于点O. 已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.