题目内容
16.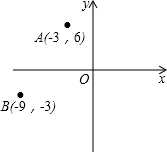 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )| A. | (-1,2) | B. | (-9,18) | C. | (-9,18)或(9,-18) | D. | (-1,2)或(1,-2) |
分析 利用位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k进行求解.
解答 解:∵A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,
∴点A的对应点A′的坐标为(-3×$\frac{1}{3}$,6×$\frac{1}{3}$)或[-3×(-$\frac{1}{3}$),6×(-$\frac{1}{3}$)],即A′点的坐标为(-1,2)或(1,-2).
故选D.
点评 本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
4.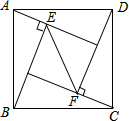 如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
 如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )
如图,在正方形ABCD中,△ABE和△CDF为直角三角形,∠AEB=∠CFD=90°,AE=CF=5,BE=DF=12,则EF的长是( )| A. | 7 | B. | 8 | C. | 7$\sqrt{2}$ | D. | 7$\sqrt{3}$ |
8.二次函数y=x2+2x-3的开口方向、顶点坐标分别是( )
| A. | 开口向上,顶点坐标为(-1,-4) | B. | 开口向下,顶点坐标为(1,4) | ||
| C. | 开口向上,顶点坐标为(1,4) | D. | 开口向下,顶点坐标为(-1,-4) |
6.化简$\frac{{m}^{2}}{m-n}$+$\frac{{n}^{2}}{n-m}$的结果是( )
| A. | m+n | B. | n-m | C. | m-n | D. | -m-n |
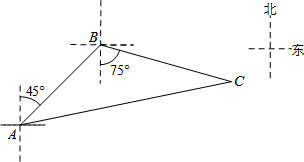 如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.
如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,求巡逻船从出发到成功拦截捕鱼船所用的时间.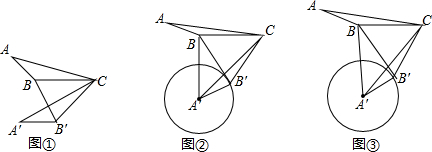
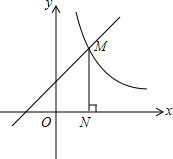 如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1
如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1