题目内容
8．二次函数y=x2+2x-3的开口方向、顶点坐标分别是（ ）| A． | 开口向上，顶点坐标为（-1，-4） | B． | 开口向下，顶点坐标为（1，4） | ||
| C． | 开口向上，顶点坐标为（1，4） | D． | 开口向下，顶点坐标为（-1，-4） |
分析 根据a＞0确定出二次函数开口向上，再将函数解析式整理成顶点式形式，然后写出顶点坐标．
解答 解：∵二次函数y=x2+2x-3的二次项系数为a=1＞0，
∴函数图象开口向上，
∵y=x2+2x-3=（x+1）2-4，
∴顶点坐标为（-1，-4）．
故选A．
点评 本题考查了二次函数的性质，主要是开口方向与顶点坐标的求解，熟记性质是解题的关键．
练习册系列答案
相关题目
如图，直线l：y=-x+1与x轴，y轴分别交于A，B两点，点P，Q是直线l上的两个动点，且点P在第二象限，点Q在第四象限，∠POQ=135°．
19．2016的倒数是（ ）
| A． | $\frac{1}{2016}$ | B． | -$\frac{1}{2016}$ | C． | 2016 | D． | -2016 |
16．
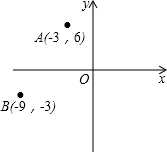如图，在平面直角坐标系中，已知点A（-3，6），B（-9，-3），以原点O为位似中心，相似比为$\frac{1}{3}$，把△ABO缩小，则点A的对应点A′的坐标是（ ）
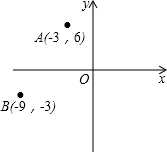如图，在平面直角坐标系中，已知点A（-3，6），B（-9，-3），以原点O为位似中心，相似比为$\frac{1}{3}$，把△ABO缩小，则点A的对应点A′的坐标是（ ）| A． | （-1，2） | B． | （-9，18） | C． | （-9，18）或（9，-18） | D． | （-1，2）或（1，-2） |
3．（-2）2的平方根是（ ）
| A． | 2 | B． | -2 | C． | ±2 | D． | $\sqrt{2}$ |
20．
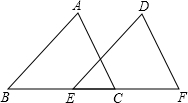如图，在△ABC和△DEF中，∠B=∠DEF，AB=DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（ ）
如图，在△ABC和△DEF中，∠B=∠DEF，AB=DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（ ）| A． | ∠A=∠D | B． | BC=EF | C． | ∠ACB=∠F | D． | AC=DF |
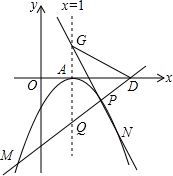如图，已知直线y=kx+b（k＞0）交抛物线y=-（x-1）2交于M、P两点，交抛物线对称轴x=1于Q（Q在x轴下方），交x轴于D，点N是点M关于对称轴x=1的对称点，延长NP交对称轴x=1于G，求证：DG=DQ．