��Ŀ����
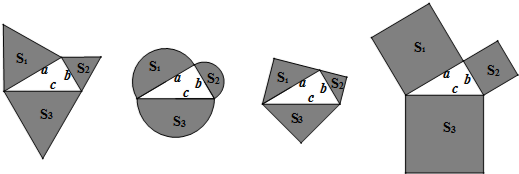
7����ѧ�-��ת�任��1����ͼ�٣��ڡ�ABC�У���ABC=130�㣬����ABC�Ƶ�C��ʱ����ת50��õ���A��B��C������BB�䣬���A��B��B�Ĵ�С��
��2����ͼ�ڣ��ڡ�ABC�У���ABC=150�㣬AB=3��BC=5������ABC�Ƶ�C��ʱ����ת60��õ���A��B��C������BB�䣬��A��ΪԲ�ģ�A��B�䳤Ϊ�뾶��Բ��
�����룺ֱ��BB�����A���λ�ù�ϵ����֤����Ľ��ۣ�
��������A��B�����߶�A��B�ij��ȣ�
��3����ͼ�ۣ��ڡ�ABC�У���ABC=����90�㣼����180�㣩��AB=m��BC=n������ABC�Ƶ�C��ʱ����ת2�½Ƕȣ�0�㣼2�£�180�㣩�õ���A��B��C������A��B��BB�䣬��A��ΪԲ�ģ�A��B�䳤Ϊ�뾶��Բ���ʣ��Ǧ���Ǧ�����ʲô����ʱ��ֱ��BB�����A�����У���˵�����ɣ�������������߶�A��B�ij��ȣ�����ýǦ���Ǧµ����Ǻ�������ĸm��n����ɵ�ʽ�ӱ�ʾ��
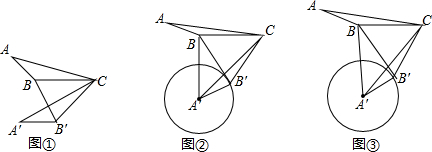
���� ��1�����ݡ�A��B��B=��A��B��C-��BB��C��ֻҪ�����BB��C���ɣ�
��2�������ۣ�ֱ��BB�����A�����У�ֻҪ֤����A��B��B=90�㼴�ɣ�������Rt��ABB���У����ù��ɶ������㼴�ɣ�
��3����ͼ���У�����+��=180��ʱ��ֱ��BB�����A�����У�ֻҪ֤����A��B��B=90�㼴�ɽ�����⣮�ڡ�CBB�������BB�䣬����Rt��A��B��B�����ù��ɶ������ɣ�
��� �⣻��1����ͼ���У��ߡ�A��B��C���ɡ�ABC��ת�õ���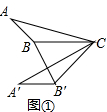
���A��B��C=��ABC=130�㣬CB=CB�䣬
���CBB��=��CB��B���ߡ�BCB��=50�㣬
���CBB��=��CB��B=65�㣬
���A��B��B=��A��B��C-��BB��C=65�㣮
��2�������ۣ�ֱ��BB�����A�����У�
���ɣ���ͼ���У��ߡ�A��B��C=��ABC=150�㣬CB=CB�䣬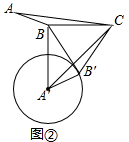
���CBB��=��CB��B���ߡ�BCB��=60�㣬
���CBB��=��CB��B=60�㣬
���A��B��B=��A��B��C-��BB��C=90�㣮
��AB���BB�䣬
��ֱ��BB�����A�����У�
������Rt��ABB���У��ߡ�AB��B=90�㣬BB��=BC=5��AB��=AB=3��
��A��B=$\sqrt{AB{��}^{2}+B��{B}^{2}}$=$\sqrt{34}$��
��3����ͼ���У�����+��=180��ʱ��ֱ��BB�����A�����У�
���ɣ��ߡ�A��B��C=��ABC=����CB=CB�䣬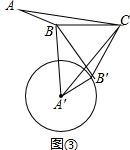
���CBB��=��CB��B���ߡ�BCB��=2�£�
���CBB��=��CB��B=$\frac{180��-2��}{2}$��
���A��B��B=��A��B��C-��BB��C=��-90��+��=180��-90��=90�㣮
��AB���BB�䣬
��ֱ��BB�����A�����У�
�ڡ�CBB���У���CB=CB��=n����BCB��=2�£�
��BB��=2•nsin�£�
��Rt��A��BB����A��B=$\sqrt{BB{��}^{2}+A��B{��}^{2}}$=$\sqrt{{m}^{2}+4{n}^{2}si{n}^{2}��}$��
���� ���⿼��Բ���ۺ��⡢��ת�����ԡ����ɶ��������ߵ��ж������������ε����ʵ�֪ʶ������Ĺؼ�������������Щ֪ʶ������⣬���������ת�����ԣ������п�ѹ���⣮

 ͨ��ѧ��Ĭд����ϵ�д�
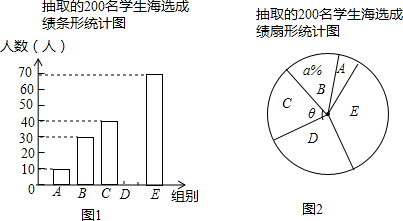
ͨ��ѧ��Ĭд����ϵ�д���ȡ��200��ѧ����ѡ�ɼ������
| ��� | ��ѡ�ɼ�x |
| A�� | 50��x��60 |
| B�� | 60��x��70 |
| C�� | 70��x��80 |
| D�� | 80��x��90 |
| E�� | 90��x��100 |
��1�����ͼ1�е�����ͳ��ͼ��������������ܰ��ʾ���뻭�ڴ�������Ӧ��ͼ�ϣ�
��2����ͼ2������ͳ��ͼ�У��DZ�ʾB��������ռ�İٷֱ�Ϊa%����a��ֵΪ15����ʾC�����ε�Բ�ĽǦȵĶ���Ϊ72�ȣ�
��3���涨��ѡ�ɼ���90�����ϣ�����90�֣���Ϊ���ŵȡ�������Ƹ�У�μ���κ�ѡ������2000��ѧ���гɼ����ŵȡ����ж����ˣ�
| A�� | $\frac{1}{2016}$ | B�� | -$\frac{1}{2016}$ | C�� | 2016 | D�� | -2016 |
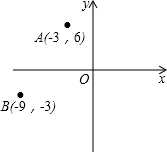 ��ͼ����ƽ��ֱ������ϵ�У���֪��A��-3��6����B��-9��-3������ԭ��OΪλ�����ģ����Ʊ�Ϊ$\frac{1}{3}$���ѡ�ABO��С�����A�Ķ�Ӧ��A��������ǣ�������
��ͼ����ƽ��ֱ������ϵ�У���֪��A��-3��6����B��-9��-3������ԭ��OΪλ�����ģ����Ʊ�Ϊ$\frac{1}{3}$���ѡ�ABO��С�����A�Ķ�Ӧ��A��������ǣ�������| A�� | ��-1��2�� | B�� | ��-9��18�� | C�� | ��-9��18����9��-18�� | D�� | ��-1��2����1��-2�� |
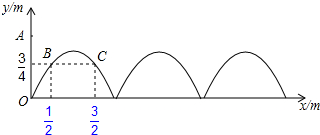
 ��ͼ��ֱ��l��y=-x+1��x�ᣬy��ֱ���A��B���㣬��P��Q��ֱ��l�ϵ��������㣬�ҵ�P�ڵڶ����ޣ���Q�ڵ������ޣ���POQ=135�㣮
��ͼ��ֱ��l��y=-x+1��x�ᣬy��ֱ���A��B���㣬��P��Q��ֱ��l�ϵ��������㣬�ҵ�P�ڵڶ����ޣ���Q�ڵ������ޣ���POQ=135�㣮 ��ͼ����������ABC�ƶ���B��ʱ�뷽����ת���ȵ���A1BC1��λ�ã�AB��A1C1�ཻ�ڵ�D��AC��A1C1��BC1�ֱ��ڵ�E��F��
��ͼ����������ABC�ƶ���B��ʱ�뷽����ת���ȵ���A1BC1��λ�ã�AB��A1C1�ཻ�ڵ�D��AC��A1C1��BC1�ֱ��ڵ�E��F�� ��ͼ����һ��Բ�����һ����������ɵļ����壬������ͼ�ǣ�������
��ͼ����һ��Բ�����һ����������ɵļ����壬������ͼ�ǣ�������