题目内容
11.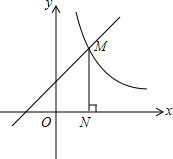 如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1
如图,一次函数y1=x+1的图象与反比例函数y2=$\frac{k}{x}$(x>0)的图象交于点M,作MN⊥x轴,N为垂足,且ON=1(1)在第一象限内,当x取何值时,y1>y2?(根据图象直接写出结果)
(2)求反比例函数的表达式.
分析 (1)根据ON=1,MN⊥x轴,得到M点的横坐标为1,代入y1=x+1=2,求得M(1,2),于是得到结论;
(2)点M在反比例函数y2=$\frac{k}{x}$(x>0)的图象上,于是得到2=$\frac{k}{1}$,求得k=2,于是得到反比例函数的表达式为y2=$\frac{2}{x}$.
解答 解:(1)∵ON=1,MN⊥x轴,
∴M点的横坐标为1,
∴当x=1时,y1=x+1=2,
∴M(1,2),
∴当x>1时,y1>y2;
(2)∵点M在反比例函数y2=$\frac{k}{x}$(x>0)的图象上,
∴2=$\frac{k}{1}$,
∴k=2,
∴反比例函数的表达式为y2=$\frac{2}{x}$.
点评 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求函数解析式,坐标与图形性质,一次函数与坐标轴的交点,以及反比例函数的图象与性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
1.下列运算正确的是( )
| A. | a2+a3=a5 | B. | (a+2b)2=a2+2ab+b2 | C. | a6÷a3=a2 | D. | (-2a3)2=4a6 |
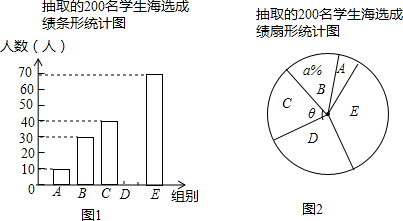
2.中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为15,表示C组扇形的圆心角θ的度数为72度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?
抽取的200名学生海选成绩分组表
| 组别 | 海选成绩x |
| A组 | 50≤x<60 |
| B组 | 60≤x<70 |
| C组 | 70≤x<80 |
| D组 | 80≤x<90 |
| E组 | 90≤x<100 |
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为15,表示C组扇形的圆心角θ的度数为72度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?

19.2016的倒数是( )
| A. | $\frac{1}{2016}$ | B. | -$\frac{1}{2016}$ | C. | 2016 | D. | -2016 |
16.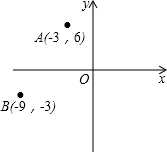 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
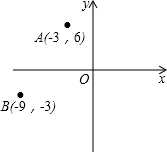 如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )
如图,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为$\frac{1}{3}$,把△ABO缩小,则点A的对应点A′的坐标是( )| A. | (-1,2) | B. | (-9,18) | C. | (-9,18)或(9,-18) | D. | (-1,2)或(1,-2) |
3.(-2)2的平方根是( )
| A. | 2 | B. | -2 | C. | ±2 | D. | $\sqrt{2}$ |
20.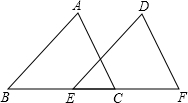 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
 如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )| A. | ∠A=∠D | B. | BC=EF | C. | ∠ACB=∠F | D. | AC=DF |
 如图,直线AB,CD被直线AE所截,AB∥CD,∠A=110°,则∠1=70度.
如图,直线AB,CD被直线AE所截,AB∥CD,∠A=110°,则∠1=70度.