题目内容
2．不等式组$\left\{\begin{array}{l}{5x-4≤2x+5}\\{2x+7＜3x+6}\end{array}\right.$的整数解的和为5．分析 求出不等式组的解集，找出解集中的所有整数解，求出之和即可．
解答 解：$\left\{\begin{array}{l}{5x-4≤2x+5①}\\{2x+7＜3x+6②}\end{array}\right.$，
由①得：x≤3；
由②得：x＞1，
故不等式组的解集为1＜x≤3，即整数解为：2，3，
则原不等式的所有整数解的和为2+3=5．
故答案为：5．
点评 此题考查了一元一次不等式组的整数解，以及一元一次不等式组的解法，求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
名校课堂系列答案
相关题目
12．计算（-4a-1）（-4a+1）的结果为（ ）
| A． | 16a2-1 | B． | -8a2-1 | C． | -4a2+1 | D． | -16a2+1 |
17．若反比例函数y=$\frac{k}{x}$的图象经过点（-1，2），则这个反比例函数的图象还经过点（ ）
| A． | （2，-1） | B． | （-$\frac{1}{2}$，1） | C． | （-2，-1） | D． | （$\frac{1}{2}$，2） |
7．化简：$\frac{{x}^{2}}{{x}^{2}+4x+4}$÷$\frac{x}{x+2}$=（ ）
| A． | x | B． | $\frac{1}{x+2}$ | C． | $\frac{x}{x+2}$ | D． | x+2 |
11．
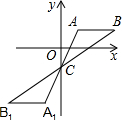如图，在平面直角坐标系中将△ABC绕点C（0，-1）旋转180°得到△A1B1C1，设点A1的坐标为（m，n），则点A的坐标为（ ）
如图，在平面直角坐标系中将△ABC绕点C（0，-1）旋转180°得到△A1B1C1，设点A1的坐标为（m，n），则点A的坐标为（ ）| A． | （-m，-n） | B． | （-m，-n-2） | C． | （-m，-n-1） | D． | （-m，-n+1） |
