题目内容
20．下列命题中，真命题是（ ）| A． | 连接矩形各边中点的四边形是菱形 | B． | 对角线垂直的四边形是菱形 | ||
| C． | 三个角相等的四边形是矩形 | D． | 两条对角线相等的四边形是矩形 |
分析 根据三角形中位线性质、矩形的性质和菱形的判定方法对A进行判断；根据菱形的判定方法对B进行判断；根据矩形的判定方法对C、D进行判断．
解答 解：A、连接矩形各边中点的四边形是菱形，所以A正确；
B、对角线垂直的平行四边形是菱形，所以B错误；
C、四个角相等的四边形是矩形，所以C错误；
D、两条对角线相等的平行四边形是矩形，所以D错误．
故选A．
点评 本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式．有些命题的正确性是用推理证实的，这样的真命题叫做定理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．
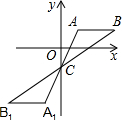如图，在平面直角坐标系中将△ABC绕点C（0，-1）旋转180°得到△A1B1C1，设点A1的坐标为（m，n），则点A的坐标为（ ）
如图，在平面直角坐标系中将△ABC绕点C（0，-1）旋转180°得到△A1B1C1，设点A1的坐标为（m，n），则点A的坐标为（ ）| A． | （-m，-n） | B． | （-m，-n-2） | C． | （-m，-n-1） | D． | （-m，-n+1） |
15．以下条件不能判别四边形ABCD是矩形的是（ ）
| A． | AB=CD，AD=BC，∠A=90° | B． | OA=OB=OC=OD | ||
| C． | AB=CD，AB∥CD，AC=BD | D． | AB=CD，AB∥CD，OA=OC，OB=OD |
5．
如图，菱形ABCD中，AB=5，BD=6，则菱形的高为（ ）
如图，菱形ABCD中，AB=5，BD=6，则菱形的高为（ ）| A． | $\frac{12}{5}$ | B． | $\frac{24}{5}$ | C． | 12 | D． | 24 |
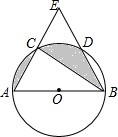如图，AB是⊙O的直径，点C，D是圆的三等分点，AC，BD的延长线交于点E，若CE=2，则⊙O中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$．