题目内容
3.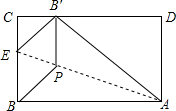 将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP,已知BC=3,CB′=1.
将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B′作B′P∥BC,交AE于点P,连接BP,已知BC=3,CB′=1.(1)求AB的长.
(2)求证:四边形BEB′P为菱形.
(3)求sin∠ABP的值.
分析 (1)设AB为x,根据折叠的性质用x表示出AB′、B′D,根据勾股定理列出方程,解方程求出x的值即可;
(2)根据折叠的性质和菱形的判定定理证明即可;
(3)根据折叠的性质和勾股定理以及正弦的概念求出sin∠CB′E,根据题意证明∠ABP=∠CB′E,即可得到答案.
解答 解:(1)设AB为x,由折叠的性质可知,AB′=AB=x,
∵四边形ABCD是矩形,CB′=1,
∴B′D=x-1,
由勾股定理得,AB′2=B′D2+AD2,即x2=(x-1)2+32,
解得,x=5,
∴AB的长为5;
(2)由折叠的性质可知,EB=EB′,PB=PB′,∠PEB=∠PEB′,
∵B′P∥BC,
∴∠BPE=∠PEB′,
∴∠PEB=∠BPE,
∴BE=BP,
∴EB=EB′=PB=PB′,
∴四边形BEB′P为菱形;
(3)设BE为y,
由折叠的性质可知,EB′=BE=y,CE=3-y,
由勾股定理得,B′E2=CE2+B′C2,即y2=(3-y)2+12,
解得,y=$\frac{5}{3}$,即BE=$\frac{5}{3}$,
∴CE=$\frac{4}{3}$,
∴sin∠CB′E=$\frac{CE}{EB′}$=$\frac{4}{5}$,
∵四边形BEB′P为菱形,
∴∠PBE=∠PB′E,
∴∠ABP=∠CB′E,
∴sin∠ABP=sin∠CB′E=$\frac{4}{5}$.
点评 本题考查的是菱形的判定、折叠的性质、勾股定理的应用和锐角三角函数的概念,掌握四条边相等的四边形是菱形、翻折变换的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.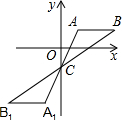 如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
 如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )| A. | (-m,-n) | B. | (-m,-n-2) | C. | (-m,-n-1) | D. | (-m,-n+1) |
18.已知二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,0),(5,0),图象上有三个点(x1,y1),(x2,y2),(x3,y3).若当x1<-1<x2<5<x3时,均有y1y2<0,y2y3<0,则下列说法中正确的是( )
| A. | a<0 | B. | x=2时,y有最大值 | C. | y1y2y3<0 | D. | 5b=4c |
15.以下条件不能判别四边形ABCD是矩形的是( )
| A. | AB=CD,AD=BC,∠A=90° | B. | OA=OB=OC=OD | ||
| C. | AB=CD,AB∥CD,AC=BD | D. | AB=CD,AB∥CD,OA=OC,OB=OD |
13. 如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )
如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )
 如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )
如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )| A. |  | B. |  | C. | 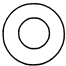 | D. | 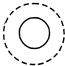 |