题目内容
1.若(3x2-2x+1)(x+b)的积不含x的一次项,求b的值.分析 先根据多项式乘以多项式法则展开,再合并同类项,根据已知得出-2b+1=0,求出即可.
解答 解:(3x2-2x+1)(x+b)
=3x3+3bx2-2x2-2bx+x+b
=3x3+(3b-2)x2+(-2b+1)x+b,
∵(3x2-2x+1)(x+b)的积不含x的一次项,
∴-2b+1=0,
∴b=$\frac{1}{2}$.
点评 本题考查了多项式乘以多项式法则的应用,能正确根据法则进行化简是解此题的关键.

练习册系列答案
相关题目
11.已知10a=20,10b=$\frac{1}{5}$,则3a÷3b的值等于( )
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
12.计算(-4a-1)(-4a+1)的结果为( )
| A. | 16a2-1 | B. | -8a2-1 | C. | -4a2+1 | D. | -16a2+1 |
9.化简a(b-4a)-(2a-b)(b-2a)的结果是( )
| A. | -3ab+b2 | B. | 3ab+b2 | C. | -8a2+ab+b2 | D. | ab-b2 |
11.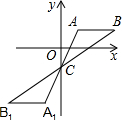 如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
 如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )| A. | (-m,-n) | B. | (-m,-n-2) | C. | (-m,-n-1) | D. | (-m,-n+1) |