题目内容
1.按一定的规律排列的两行数:| n(n是奇数,且n≥3) | 3 | 5 | 7 | 9 | … |
| m(m是偶数,且m≥4) | 4 | 12 | 24 | 40 | … |
分析 根据给定的数据分析m、n之间的关系,由此可得出结论.
解答 解:观察,发现规律:当n=3时,m=$\frac{1}{2}$(32-1)=4;当n=5时,m=$\frac{1}{2}$(52-1)=12;当n=7时,m=$\frac{1}{2}$(72-1)=24;当n=9时,m=$\frac{1}{2}$(92-1)=40;…,
∴m=$\frac{1}{2}$(n2-1).
故答案为:m=$\frac{1}{2}$(n2-1).
点评 本题考查了规律型中的数字的变化类,解题的关键是找出m、n之间的关系.本题属于基础题,解决该题型题目时,根据给定等式找出变化规律是关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
11.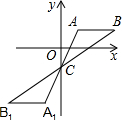 如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
 如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )
如图,在平面直角坐标系中将△ABC绕点C(0,-1)旋转180°得到△A1B1C1,设点A1的坐标为(m,n),则点A的坐标为( )| A. | (-m,-n) | B. | (-m,-n-2) | C. | (-m,-n-1) | D. | (-m,-n+1) |
13. 如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )
如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )
 如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )
如图,将一个小球摆放在圆柱上,该几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
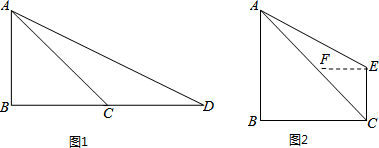
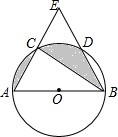 如图,AB是⊙O的直径,点C,D是圆的三等分点,AC,BD的延长线交于点E,若CE=2,则⊙O中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$.
如图,AB是⊙O的直径,点C,D是圆的三等分点,AC,BD的延长线交于点E,若CE=2,则⊙O中阴影部分的面积为$\frac{4}{3}$π-$\sqrt{3}$.