Question

9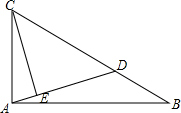．如图，已知点D是Rt△ABC的斜边BC上的一点，tanB=$\frac{1}{k}$，BC=（k+1）BD，CE⊥AD，则$\frac{AE}{CE}$=$\frac{1}{{k}^{2}}$（用含k的代数式表示）．

Answer 1

分析 根据题意结合平行线的性质得出$\frac{BD}{DC}$=$\frac{BF}{AF}$=$\frac{1}{k}$，进而利用锐角三角函数关系得出tan∠ACE=tan∠DAF=$\frac{AE}{EC}$=$\frac{DF}{AF}$，进而得出答案．

解答 解：过点D作DF⊥AB于点F，
∵∠CAB=90°，DF⊥AB，
∴AC∥DF，
∴$\frac{BD}{CD}$=$\frac{BF}{AF}$，
∵BC=（k+1）BD，
∴$\frac{BD}{DC}$=$\frac{BF}{AF}$=$\frac{1}{k}$，
∴AF=k•BF
∵tanB=$\frac{1}{k}$，
∴$\frac{DF}{FB}$=$\frac{1}{k}$，
∴DF=$\frac{1}{k}$FB，
∴$\frac{DF}{AF}$=$\frac{\frac{1}{k}FB}{AF}$=$\frac{\frac{1}{k}FB}{k•FB}$=$\frac{1}{{k}^{2}}$，
∵CE⊥AD，
∴tan∠ACE=$\frac{AE}{EC}$，
∵∠CAE+∠ACE=90°，∠CAE+∠DAB=90°，
∴∠ACE=∠DAF，
∴tan∠ACE=tan∠DAF=$\frac{AE}{EC}$=$\frac{DF}{AF}$=$\frac{1}{{k}^{2}}$．
故答案为：$\frac{1}{{k}^{2}}$．

点评 此题主要考查了平行线分线段成比例定理以及锐角三角函数关系等知识，正确得出tan∠ACE=tan∠DAF=$\frac{AE}{EC}$=$\frac{DF}{AF}$是解题关键．