题目内容
14.小明用一块含30°的直角三角板在已知线段AB上作出△ABC(如图所示).若AB=6,则△ABC的面积为3$\sqrt{3}$.
分析 根据∠A=∠B得△ACB是等腰三角形,作CD⊥AB垂足为D,设CD=x则AC=2x,在RT△ACD中利用勾股定理求出x,然后代入三角形面积公式即可.
解答  解:如图作CD⊥AB垂足为D,设AD=x,
解:如图作CD⊥AB垂足为D,设AD=x,
∵∠A=∠B=30°,
∴CA=CB=2x,
∴AD=DB=$\frac{1}{2}$AB=3,
在RT△ACD中,AC2=AD2+CD2,
∴4x2=x2+32,
∵x>0,
∴x=$\sqrt{3}$即CD=$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$•AB•CD=3$\sqrt{3}$.
故答案为3$\sqrt{3}$.
点评 本题考查等腰三角形的判定和性质、勾股定理、三角形面积公式以及直角三角形中30度角的性质,利用勾股定理求出三角形的高是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如果你将一张等腰三角形的纸片折一次,使得折痕平分这个等腰三角形的面积,这样的折纸方法种类有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 无数种 |
2.下列图形中,既是轴对称图形,又是中心对称图形的是( )?
| A. |  | B. |  | C. |  | D. |  |
6.若反比例函数y=$\frac{k}{x}$的图象经过点(-1,3),则这个反比例函数的图象还经过点( )
| A. | (3,-1) | B. | (-$\frac{1}{3}$,1) | C. | (-3,-1) | D. | ($\frac{1}{3}$,2) |

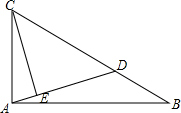 如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{k}$,BC=(k+1)BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{{k}^{2}}$(用含k的代数式表示).
如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{k}$,BC=(k+1)BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{{k}^{2}}$(用含k的代数式表示).

 如图所示放置的三角板,把三角板较长的直角边从水平状态开始,在平面上沿着直线BC滚动一周,B点转动的角度是210°.
如图所示放置的三角板,把三角板较长的直角边从水平状态开始,在平面上沿着直线BC滚动一周,B点转动的角度是210°.