题目内容
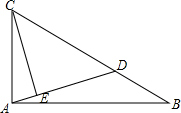
1. 在△ABC中,∠B=2∠C,AC=4$\sqrt{5}$,AB=5,求BC的长.
在△ABC中,∠B=2∠C,AC=4$\sqrt{5}$,AB=5,求BC的长.
分析 作∠ABC的角平分线BD交AC于点D,易证△CDB是等腰三角形和△ADB∽△ABC,由相似三角形的性质可求出AD的长,进而可求BD的长,再由对应边的比值相等即可求出BD的长.
解答 解:作∠ABC的角平分线BD交AC于点D,
∴∠ABD=∠DBC=$\frac{1}{2}$∠ABC,
∵∠B=2∠C,
∴∠C=∠DBC,
∴BD=CD,
∵∠A=∠A,
∴△ADB∽△ABC,
∴$\frac{AD}{AB}=\frac{AB}{AC}=\frac{DB}{BC}$,
设AD=x,
∴$\frac{x}{5}=\frac{5}{4\sqrt{5}}$,
∴AD=$\frac{5\sqrt{5}}{4}$,
∴则CD=BD=4$\sqrt{5}$-$\frac{5\sqrt{5}}{4}$=$\frac{11\sqrt{5}}{4}$,
∵$\frac{AB}{AC}=\frac{DB}{BC}$,
∴$\frac{5}{4\sqrt{5}}=\frac{\frac{11}{4}\sqrt{5}}{BD}$,
∴BD=11.
点评 本题考查了相似三角形的判定和性质以及等腰三角形的判定和性质,题目的设计很新颖,是非常不错的一道中考题,解题的关键是证明出CD=DB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
 如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )
如图,已知∠ABC,小彬借助一把没有刻度且等宽的直尺,按如图的方法画出了∠ABC的平分线BP.他这样做的依据是( )| A. | 在一个角的内部,且到角两边的距离相等的点在这个角的平分线上 | |
| B. | 角平分线上的点到这个角两边的距离相等 | |
| C. | 三角形三条角平分线的交点到三条边的距离相等 | |
| D. | 以上均不正确 |
16. 为了响应绿色消费,保护环境的号召,某品牌汽车4S店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共15辆,以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息:
为了响应绿色消费,保护环境的号召,某品牌汽车4S店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共15辆,以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息:
(1)若经营者的购买资金为408万元,则两种型号的汽车各几辆?
(2)假设每台电动汽车每公里的用电费用为0.20元,每行驶5万公里必须更换一次车载电池1.8万元,且两种汽车最大行驶里程均为30万公里,如果你是购车者,从购车和养车总成本的角度考虑,将会选购哪一种型号的汽车?并说明理由.
 为了响应绿色消费,保护环境的号召,某品牌汽车4S店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共15辆,以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息:
为了响应绿色消费,保护环境的号召,某品牌汽车4S店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共15辆,以满足广大支持环保的购车者的需求.市场营销人员经过市场调查得到如下信息:| 成本价(万元/辆) | 售价(万元/辆) | |
| A型 | 20 | 22 |
| B型 | 32 | 35 |
(2)假设每台电动汽车每公里的用电费用为0.20元,每行驶5万公里必须更换一次车载电池1.8万元,且两种汽车最大行驶里程均为30万公里,如果你是购车者,从购车和养车总成本的角度考虑,将会选购哪一种型号的汽车?并说明理由.
6.若反比例函数y=$\frac{k}{x}$的图象经过点(-1,3),则这个反比例函数的图象还经过点( )
| A. | (3,-1) | B. | (-$\frac{1}{3}$,1) | C. | (-3,-1) | D. | ($\frac{1}{3}$,2) |
13.矩形具有而平行四边形不具有的性质是( )
| A. | 两组对边分别平行 | B. | 两组对角分别相等 | ||
| C. | 对角线相等 | D. | 对角线互相垂直 |
10. 如图,在三角形ABC中,已知AB=AC,D为BC边上的一点,且AB=BD,AD=CD,则∠ABC等于( )
如图,在三角形ABC中,已知AB=AC,D为BC边上的一点,且AB=BD,AD=CD,则∠ABC等于( )
 如图,在三角形ABC中,已知AB=AC,D为BC边上的一点,且AB=BD,AD=CD,则∠ABC等于( )
如图,在三角形ABC中,已知AB=AC,D为BC边上的一点,且AB=BD,AD=CD,则∠ABC等于( )| A. | 36° | B. | 38° | C. | 40° | D. | 45° |
11. 如图,用8块相同的小长方形拼成一个大长方形,则大长方形对角线的长为( )
如图,用8块相同的小长方形拼成一个大长方形,则大长方形对角线的长为( )
 如图,用8块相同的小长方形拼成一个大长方形,则大长方形对角线的长为( )
如图,用8块相同的小长方形拼成一个大长方形,则大长方形对角线的长为( )| A. | 10$\sqrt{52}$cm | B. | 72cm | C. | 10$\sqrt{53}$cm | D. | 10cm |
 如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{k}$,BC=(k+1)BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{{k}^{2}}$(用含k的代数式表示).
如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{k}$,BC=(k+1)BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{{k}^{2}}$(用含k的代数式表示).