题目内容
18. 如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )
如图,在等腰△ABC中,AB=AC,∠A=20°,AB上一点D使AD=BC,过点D作DE∥BC且DE=AB,连接EC,则∠DCE的度数为( )| A. | 80° | B. | 70° | C. | 60° | D. | 45° |
分析 连接AE.根据ASA可证△ADE≌△CBA,根据全等三角形的性质可得AE=AC,∠AED=∠BAC=20°,根据等边三角形的判定可得△ACE是等边三角形,根据等腰三角形的判定可得△DCE是等腰三角形,再根据三角形内角和定理和角的和差关系即可求解.
解答 解:如图所示,连接AE.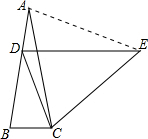
∵AE=DE,
∴∠ADE=∠DAE,
∵DE∥BC,
∴∠DAE=∠ADE=∠B,
∵AB=AC,∠BAC=20°,
∴∠DAE=∠ADE=∠B=∠ACB=80°,
在△ADE与△CBA中,
$\left\{\begin{array}{l}{∠DAE=∠ACB}\\{AD=BC}\\{∠ADE=∠B}\end{array}\right.$,
∴△ADE≌△CBA(ASA),
∴AE=AC,∠AED=∠BAC=20°,
∵∠CAE=∠DAE-∠BAC=80°-20°=60°,
∴△ACE是等边三角形,
∴CE=AC=AE=DE,∠AEC=∠ACE=60°,
∴△DCE是等腰三角形,
∴∠CDE=∠DCE,
∴∠DEC=∠AEC-∠AED=40°,
∴∠DCE=∠CDE=(180-40°)÷2=70°.
故选B.
点评 考查了等腰三角形的性质,全等三角形的判定和性质,等边三角形的判定和性质,等腰三角形的判定和性质,三角形内角和定理,平行线的性质,综合性较强,有一定的难度.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
6.若反比例函数y=$\frac{k}{x}$的图象经过点(-1,3),则这个反比例函数的图象还经过点( )
| A. | (3,-1) | B. | (-$\frac{1}{3}$,1) | C. | (-3,-1) | D. | ($\frac{1}{3}$,2) |
13.矩形具有而平行四边形不具有的性质是( )
| A. | 两组对边分别平行 | B. | 两组对角分别相等 | ||
| C. | 对角线相等 | D. | 对角线互相垂直 |
10. 如图,在三角形ABC中,已知AB=AC,D为BC边上的一点,且AB=BD,AD=CD,则∠ABC等于( )
如图,在三角形ABC中,已知AB=AC,D为BC边上的一点,且AB=BD,AD=CD,则∠ABC等于( )
 如图,在三角形ABC中,已知AB=AC,D为BC边上的一点,且AB=BD,AD=CD,则∠ABC等于( )
如图,在三角形ABC中,已知AB=AC,D为BC边上的一点,且AB=BD,AD=CD,则∠ABC等于( )| A. | 36° | B. | 38° | C. | 40° | D. | 45° |
7. 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠ACB=65°,则∠1的度数是( )
如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠ACB=65°,则∠1的度数是( )
 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠ACB=65°,则∠1的度数是( )
如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠ACB=65°,则∠1的度数是( )| A. | 25° | B. | 35° | C. | 50° | D. | 65° |
 如图,AB∥DC,且AD∥BC,∠α=50°,求∠C的度数.
如图,AB∥DC,且AD∥BC,∠α=50°,求∠C的度数.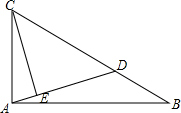 如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{k}$,BC=(k+1)BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{{k}^{2}}$(用含k的代数式表示).
如图,已知点D是Rt△ABC的斜边BC上的一点,tanB=$\frac{1}{k}$,BC=(k+1)BD,CE⊥AD,则$\frac{AE}{CE}$=$\frac{1}{{k}^{2}}$(用含k的代数式表示).