题目内容
12.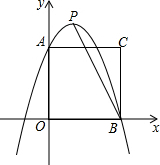 如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)
如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)(1)求抛物线的解析式;
(2)点M为抛物线上一点,恰使△MOA≌△MOB,求点M的坐标;
(3)y轴上是否存在一点N,恰好使得△PNB为直角三角形?若存在,直接写出满足条件的所有点N的坐标;若不存在,请说明理由.
分析 (1)由正方形的性质可知OA=OB=3,从而得到点A的坐标,设抛物线的解析式为y=a(x-1)2+4,把A(0,3)代入可求得a的值,从而得到抛物线的解析式;
(2)由全等三角形对应边相等可知MA=BM,从而可知点M在AB的垂直平分线上,故此点M为直线OC与抛物线的交点,然后求得直线OC与抛物线的交点坐标即可;
(3)设N(0,t).分为∠PNB=90、∠NPB=90°、∠PBN=90°三种情况画出图形,然后依据相似三角形对应边成比例列出关于t的方程求解即可.
解答 解:(1)∵正方形的边长为3,
∴A(0,3),B(3,0).
设抛物线的解析式为y=a(x-1)2+4.
∵把A(0,3)代入得:a+4=3,解得a=-1,
∴抛物线的解析式为y=-(x-1)2+4=-x2+2x+3.
(2)如图1所示:
∵△MOA≌△MOB,
∴AM=BM.
∴点M在AB的垂直平分线上.
∵OACB为正方形,
∴OC为AB的垂直平分线.
设OC的解析式为y=kx,
∵将C(3,3)代入得:3k=3,解得:k=1,
∴直线OC的解析式为y=x.
由y=x与y=-x2+2x+3得:x=-x2+2x+3,解得:x1=$\frac{1+\sqrt{13}}{2}$,x2=$\frac{1-\sqrt{13}}{2}$.
∴M($\frac{1+\sqrt{13}}{2}$,$\frac{1+\sqrt{13}}{2}$),M′($\frac{1-\sqrt{13}}{2}$,$\frac{1-\sqrt{13}}{2}$).
∴点M的坐标为($\frac{1+\sqrt{13}}{2}$,$\frac{1+\sqrt{13}}{2}$)或($\frac{1-\sqrt{13}}{2}$,$\frac{1-\sqrt{13}}{2}$).
(3)设N(0,t).
①当∠PNB=90时,如图2所示.连接PN、BN,过点P作PM⊥y轴,垂足为M.
由△PMN∽△NOB,得:$\frac{1}{t}=\frac{4-t}{3}$,解得:t1=1,t2=3.
②当∠NPB=90°时.
如图3所示;连接PN、BN,过点P作x轴的平行线,交BC延长线与点M.
由△PMN∽△NOB,得:$\frac{1}{4}=\frac{4-t}{2}$,解得:t=$\frac{7}{2}$.
③当∠PBN=90°时,如图4所示,过点P作x轴的平行线,交BC延长线与点M.
由△PMB∽△NOB得:$\frac{2}{-t}=\frac{4}{3}$,解得:t=-$\frac{3}{2}$.
综上所述,点N的坐标为(0,1)、(0,3)、(0,$\frac{7}{2}$)、(0,-$\frac{3}{2}$).
点评 本题主要考查的是二次函数的综合应用,解答本题需要熟练掌握待定系数法求函数解析式的步骤和方法、二次函数表达式的三种基本形式、相似三角形的性质、正方形的性质,分类讨论是解题的关键.

| A. | 1,1,$\sqrt{2}$ | B. | 12,16,20 | C. | 1,$\frac{4}{3}$,$\frac{5}{3}$ | D. | 1,2,2 |
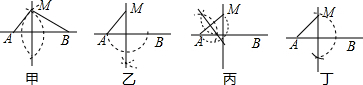
| A. | 甲、乙 | B. | 乙、丙 | C. | 丙、丁 | D. | 甲、乙、丙 |
| A. | y<0 | B. | y≤0 | C. | y>0 | D. | y≥0 |
 如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则平行四边形ABCD的周长为18.
如图,在平行四边形ABCD中,AD=2AB,CE平分∠BCD交AD边于点E,且AE=3,则平行四边形ABCD的周长为18.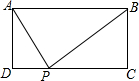 如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=1或4或2.5.
如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=1或4或2.5.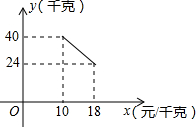 某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示,该经销商想要每天获得150元的销售利润,销售价应定为多少?列出关于x方程是(x-10)(-2x+60)=150(不需化简和解方程).
某经销商销售一种产品,这种产品的成本价为10元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克,且10≤x≤18)之间的函数关系如图所示,该经销商想要每天获得150元的销售利润,销售价应定为多少?列出关于x方程是(x-10)(-2x+60)=150(不需化简和解方程).
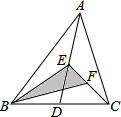 如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3.
如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3.