题目内容
7．某学习小组中有甲、乙、丙、丁四位同学，为解决尺规作图：“过直线AB外一点M，作一直线垂直于直线AB”，各自提供了如下四种方案，其中正确的是（ ）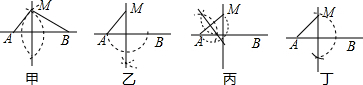
| A． | 甲、乙 | B． | 乙、丙 | C． | 丙、丁 | D． | 甲、乙、丙 |
分析 根据作已知线段的垂直平分线可对甲、乙进行判断；根据圆周角定理对乙进行判断．
解答 解：甲作了AB垂直平分过点M的线段；乙作了线段AB的垂直平分线；丙作了以AM为直径的圆；丁的作法不明确．
故选D．
点评 本题考查了基本作图：作一条线段等于已知线段；作一个角等于已知角；作已知线段的垂直平分线；作已知角的角平分线；过一点作已知直线的垂线．
练习册系列答案
相关题目
如图，在?ABCD中，对角线AC、BD相交于点O．如果AC=6，BD=4，AB=x，那么x的取值范围是1＜x＜5．
18．
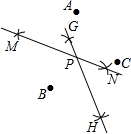如图所示的是A、B、C、D三点，按如下步骤作图：①先分别以A、B两点为圆心，以大于$\frac{1}{2}$AB的长为半径作弧，两弧相交于M、N两点，作直线MN；②再分别以B、C两点为圆心，以大于$\frac{1}{2}BC$的长为半径作弧，两弧相交于G、H两点，作直线GH，GH与MN交于点P，若∠BAC=66°，则∠BPC等于（ ）
如图所示的是A、B、C、D三点，按如下步骤作图：①先分别以A、B两点为圆心，以大于$\frac{1}{2}$AB的长为半径作弧，两弧相交于M、N两点，作直线MN；②再分别以B、C两点为圆心，以大于$\frac{1}{2}BC$的长为半径作弧，两弧相交于G、H两点，作直线GH，GH与MN交于点P，若∠BAC=66°，则∠BPC等于（ ）| A． | 100° | B． | 120° | C． | 132° | D． | 140° |
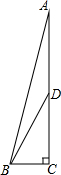（1）计算：sin30°+3tan60°-cos245°．
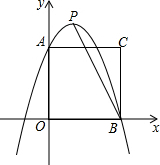如图所示，将一边长为3的正方形放置到平面直角坐标系中，其顶点A、B均落在坐标轴上，一抛物线过点A、B，且顶点为P（1，4）
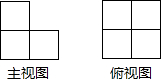由若干个形状大小相同的小正方体木块组成的几何体的主视图和俯视图如下，则这样的小正方形木块至少有（ ）块．
16．下列运算正确的是（ ）
| A． | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B． | $\sqrt{4\frac{1}{9}}=2\frac{1}{3}$ | C． | $\sqrt{{{（{2-\sqrt{5}}）}^2}}=2-\sqrt{5}$ | D． | $\frac{1}{{2-\sqrt{3}}}=2+\sqrt{3}$ |