题目内容
2.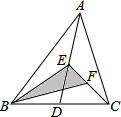 如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3.
如图,AD是△ABC的中线,点E、F分别为AD、CE的中点,且△ABC的面积是12,则△BEF的面积是3.
分析 根据三角形的中线把三角形分成两个面积相等的三角形解答.
解答 解:∵点D是BC的中点,
∴S△ABD=S△ACD=$\frac{1}{2}$S△ABC=$\frac{1}{2}$×12=6,
∵点E是AD的中点,
∴S△BDE=$\frac{1}{2}$S△ABD=$\frac{1}{2}$×6=3,
S△CDE=$\frac{1}{2}$S△ACD=$\frac{1}{2}$×6=3,
∴S△BCE=S△BDE+S△CDE=3+3=6,
∵点F是CE的中点,
∴S△BEF=$\frac{1}{2}$S△BCE=$\frac{1}{2}$×6=3.
故答案为:3.
点评 本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
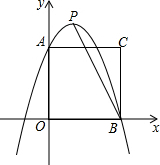 如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)
如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)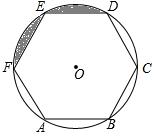 如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1.
如图,正六边形ABCDEF内接于⊙O,⊙O的半径为1. 如图,在四边形ABCD中,AB=24,BC=20,CD=15,AD=7,∠C=90°,试求∠A的度数.
如图,在四边形ABCD中,AB=24,BC=20,CD=15,AD=7,∠C=90°,试求∠A的度数. 如图,在圆心角为90°的扇形OAB中,半径OA=4cm,C为$\widehat{AB}$的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为2π+2$\sqrt{2}$-2cm2.
如图,在圆心角为90°的扇形OAB中,半径OA=4cm,C为$\widehat{AB}$的中点,D,E分别是OA,OB的中点,则图中阴影部分的面积为2π+2$\sqrt{2}$-2cm2.