题目内容
 如图所示,△ABC是等边三角形,延长BC至E,延长BA至F,使AF=BE,连接CF、EF,过点F作直线FD⊥CE
如图所示,△ABC是等边三角形,延长BC至E,延长BA至F,使AF=BE,连接CF、EF,过点F作直线FD⊥CE于D,求证:FD为∠CFE的平分线.
考点:全等三角形的判定与性质,等腰三角形的判定与性质,等边三角形的性质
专题:证明题
分析:延长BE到G,使EG=BC,连接FG,证明△BCF≌△GEF,得出CF=FE,利用等腰三角形的性质可得出结论.
解答: 证明:延长BE到G,使EG=BC,连接FG,
证明:延长BE到G,使EG=BC,连接FG,
∵AF=BE,△ABC为等边三角形,
∴BF=BG,∠ABC=60°,
∴△GBF也是等边三角形.
在△BCF和△GEF中,
,
∴△BCF≌△GEF(SAS),
∴FC=EF,
∵FD⊥CE,
∴FD为∠CFE的平分线.
 证明:延长BE到G,使EG=BC,连接FG,
证明:延长BE到G,使EG=BC,连接FG,∵AF=BE,△ABC为等边三角形,
∴BF=BG,∠ABC=60°,
∴△GBF也是等边三角形.
在△BCF和△GEF中,
|
∴△BCF≌△GEF(SAS),
∴FC=EF,
∵FD⊥CE,
∴FD为∠CFE的平分线.
点评:本题主要考查等边三角形的性质、等腰三角形的判定和性质及全等三角形的判定,构造三角形证明全等是解题的关键.

练习册系列答案
相关题目
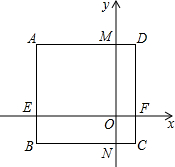 长方形ABCD在平面直角坐标系中的位置如图所示,AD∥x轴,AB∥y轴,已知长方形ABCD的长为3,宽为2,且点A的坐标为(-1.5,2),求长方形的顶点B、C、D的坐标及矩形AEOM的面积.
长方形ABCD在平面直角坐标系中的位置如图所示,AD∥x轴,AB∥y轴,已知长方形ABCD的长为3,宽为2,且点A的坐标为(-1.5,2),求长方形的顶点B、C、D的坐标及矩形AEOM的面积.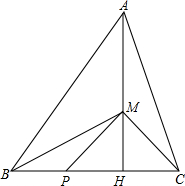 如图,已知在△ABC中,AB=5,BC=4,AC=
如图,已知在△ABC中,AB=5,BC=4,AC=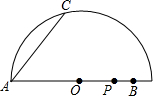 已知线段AB为半圆O的直径,AB=10cm,AC=6cm,点P为AB上一动点,P由B向A以2cm/s的速度运动,到达A点后停止运动.设P点的运动时间为t秒,当t为何值时,△ACP为等腰三角形?
已知线段AB为半圆O的直径,AB=10cm,AC=6cm,点P为AB上一动点,P由B向A以2cm/s的速度运动,到达A点后停止运动.设P点的运动时间为t秒,当t为何值时,△ACP为等腰三角形? 如图,已知:∠FNM=∠B,∠FMN=∠C,求证:∠A=∠F.
如图,已知:∠FNM=∠B,∠FMN=∠C,求证:∠A=∠F.