题目内容
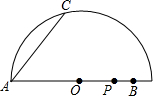 已知线段AB为半圆O的直径,AB=10cm,AC=6cm,点P为AB上一动点,P由B向A以2cm/s的速度运动,到达A点后停止运动.设P点的运动时间为t秒,当t为何值时,△ACP为等腰三角形?
已知线段AB为半圆O的直径,AB=10cm,AC=6cm,点P为AB上一动点,P由B向A以2cm/s的速度运动,到达A点后停止运动.设P点的运动时间为t秒,当t为何值时,△ACP为等腰三角形?考点:等腰三角形的判定,勾股定理,圆周角定理
专题:
分析:连接BC,可求得BC=8,再分AP=CP、AP=AC和AC=PC三种情况讨论,①当AP=CP时,过P作PD⊥AC,可知P为AB中点,可求得t,②当AP=AC时,AP=6,可求出t,③当AC=PC时,过C作CE⊥AB,利用三角函数可求出AE的长,可求得t.
解答:解:
连接BC,则∠ACB=90°,
可求得BC=8,
①当AP=CP时,如图1,过P作PD⊥AC,则D为AC中点,且PD∥BC,所以P为AB中点,
所以PB=5,即2t=5,解得t=2.5;

②当AP=AC时,AP=6,则PB=10-6=4,即2t=4,解得t=2,
③当AC=PC时,如图2,过C作CE⊥AB,则cos∠CAE=
=
,即
=
,解得AE=3.6,
所以AP=2AE=7.2,所以BP=10-7.2=2.8,即2t=2.8,解得t=1.4,

综上可知当t为2.5、3.6和1.4时,△ACP为等腰三角形.
连接BC,则∠ACB=90°,
可求得BC=8,
①当AP=CP时,如图1,过P作PD⊥AC,则D为AC中点,且PD∥BC,所以P为AB中点,
所以PB=5,即2t=5,解得t=2.5;

②当AP=AC时,AP=6,则PB=10-6=4,即2t=4,解得t=2,
③当AC=PC时,如图2,过C作CE⊥AB,则cos∠CAE=
| AE |
| AC |
| AC |
| AB |
| AE |
| 6 |
| 6 |
| 10 |
所以AP=2AE=7.2,所以BP=10-7.2=2.8,即2t=2.8,解得t=1.4,

综上可知当t为2.5、3.6和1.4时,△ACP为等腰三角形.
点评:本题主要考查等腰三角形的判定和性质,分三种情况分别讨论是解题的关键.

练习册系列答案
相关题目

 如图所示,△ABC是等边三角形,延长BC至E,延长BA至F,使AF=BE,连接CF、EF,过点F作直线FD⊥CE
如图所示,△ABC是等边三角形,延长BC至E,延长BA至F,使AF=BE,连接CF、EF,过点F作直线FD⊥CE 如图所示,过?ABCD的对角线的交点O任意画一条直线l,分别交AD、BC于点E、F,l将平行四边形分成两个四边形,这两个四边形是否关于点O成中心对称?请说明理由.
如图所示,过?ABCD的对角线的交点O任意画一条直线l,分别交AD、BC于点E、F,l将平行四边形分成两个四边形,这两个四边形是否关于点O成中心对称?请说明理由.