题目内容
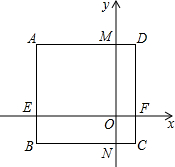 长方形ABCD在平面直角坐标系中的位置如图所示,AD∥x轴,AB∥y轴,已知长方形ABCD的长为3,宽为2,且点A的坐标为(-1.5,2),求长方形的顶点B、C、D的坐标及矩形AEOM的面积.
长方形ABCD在平面直角坐标系中的位置如图所示,AD∥x轴,AB∥y轴,已知长方形ABCD的长为3,宽为2,且点A的坐标为(-1.5,2),求长方形的顶点B、C、D的坐标及矩形AEOM的面积.考点:坐标与图形性质
专题:数形结合
分析:由于AD∥x轴,AB∥y轴,点A的坐标为(-1.5,2),利用坐标与点到坐标轴的距离的关系得到AM=1.5,AE=2,则有AB=CD=3,AD=BC=2,所以BE=CF=1,MD=CN=0.5,根据根据各象限点的坐标特征写出B、C、D的坐标,利用矩形面积公式计算矩形AEOM的面积.
解答:解:∵AD∥x轴,AB∥y轴,点A的坐标为(-1.5,2),
∴AM=1.5,AE=2,
∵长方形ABCD的长为3,宽为2,
∴AB=CD=3,AD=BC=2,
∴BE=CF=1,MD=CN=0.5,
∴B点坐标为(-1.5,-1),C点坐标为(0.5,-1),D点坐标为(0.5,2);
故矩形AEOM的面积=1.5×2=3.
∴AM=1.5,AE=2,
∵长方形ABCD的长为3,宽为2,
∴AB=CD=3,AD=BC=2,
∴BE=CF=1,MD=CN=0.5,
∴B点坐标为(-1.5,-1),C点坐标为(0.5,-1),D点坐标为(0.5,2);
故矩形AEOM的面积=1.5×2=3.
点评:本题考查了坐标与图形性质:利用点的坐标特征计算相应的线段长和判断线段与坐标轴的位置关系;记住各象限内点的坐标特征和坐标上点的坐标特征.

练习册系列答案
相关题目
已知6x-4y-1=9,则2y-3x的值为( )
| A、4 | B、-4 | C、5 | D、-5 |
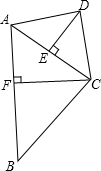 如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12.
如图,四边形ABCD中,AC平分∠BAD,BC⊥AC,CD⊥AD,AB=18,AC=12. 如图所示,△ABC是等边三角形,延长BC至E,延长BA至F,使AF=BE,连接CF、EF,过点F作直线FD⊥CE
如图所示,△ABC是等边三角形,延长BC至E,延长BA至F,使AF=BE,连接CF、EF,过点F作直线FD⊥CE