题目内容
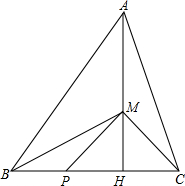 如图,已知在△ABC中,AB=5,BC=4,AC=
如图,已知在△ABC中,AB=5,BC=4,AC=| 17 |
①求CH的长;
②设BP=x,S△MPC=y,求y关于x的函数解析式,并写出函数的定义域;
③当△MPC为以MC为腰的等腰三角形时,求BP的长.
考点:相似三角形的判定与性质
专题:
分析:(1)根据勾股定理直接列出方程求解;
(2)首先求出MH的长,表示出PC的长,进而求出△MPC的面积;
(3)运用分类讨论的数学思想,按MP为等腰三角形的腰或底,分两种情况求出PC的长,进而求出BP的长.
(2)首先求出MH的长,表示出PC的长,进而求出△MPC的面积;
(3)运用分类讨论的数学思想,按MP为等腰三角形的腰或底,分两种情况求出PC的长,进而求出BP的长.
解答: 解:(1)设CH=x,则BH=4-x;
解:(1)设CH=x,则BH=4-x;
∵AH⊥BC,∴AB2-BH2=AH2,AC2-CH2=AH2,
故AB2-BH2=AC2-CH2,即52-(4-x)2=(
)2-x2,
化简整理得:8x=8,x=1;
故CH的长为1;
(2)由(1)知CH=1,故BH=4-1=3;
∵AH2=AB2-BH2=52-32=16,
∴AH=4,
∵∠ABC的平分线交AH于点M,
∴
=
,
而AB=5,BH=4-1=3,AM=4-MH,
∴
=
,解得MH=
;
∵BP=x,
∴CP=4-x,S△MPC=
PC•MH=
(4-x)×
,
即y=-
x+3,0≤x<4;
(3)当△MPC为以MC为腰的等腰三角形时,
若MP为腰,
∵MH⊥PC,
∴PH=HC=1,
BP=4-2=2;
若MP为底时,PC=MC;
∵MC=
=
=
=
,∴BP=BC-PC=4-
∴当△MPC为以MC为腰的等腰三角形时,BP的长为2或4-
.
 解:(1)设CH=x,则BH=4-x;
解:(1)设CH=x,则BH=4-x;∵AH⊥BC,∴AB2-BH2=AH2,AC2-CH2=AH2,
故AB2-BH2=AC2-CH2,即52-(4-x)2=(
| 17 |
化简整理得:8x=8,x=1;
故CH的长为1;
(2)由(1)知CH=1,故BH=4-1=3;
∵AH2=AB2-BH2=52-32=16,
∴AH=4,
∵∠ABC的平分线交AH于点M,
∴
| AB |
| BH |
| AM |
| MH |
而AB=5,BH=4-1=3,AM=4-MH,
∴
| 5 |
| 3 |
| 4-MH |
| MH |
| 3 |
| 2 |
∵BP=x,
∴CP=4-x,S△MPC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
即y=-
| 3 |
| 4 |
(3)当△MPC为以MC为腰的等腰三角形时,
若MP为腰,
∵MH⊥PC,
∴PH=HC=1,
BP=4-2=2;
若MP为底时,PC=MC;
∵MC=
12+(
|
1+
|
|
| ||
| 2 |
| ||
| 2 |
∴当△MPC为以MC为腰的等腰三角形时,BP的长为2或4-
| ||
| 2 |
点评:该题主要考查了勾股定理、角平分线的性质及其应用问题;同时还渗透了对等腰三角形的定义等知识的考查,对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
化简-{+[-(x-y)]}+{-(x+y)}可得( )
| A、2x | B、2x+2y |
| C、-2y | D、2x-2y |
 如图所示,△ABC是等边三角形,延长BC至E,延长BA至F,使AF=BE,连接CF、EF,过点F作直线FD⊥CE
如图所示,△ABC是等边三角形,延长BC至E,延长BA至F,使AF=BE,连接CF、EF,过点F作直线FD⊥CE