题目内容
18.“小组合作学习”成为我区推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“小组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
请结合图中信息解答下列问题:
(1)小组合作学习前学生学习兴趣为“高”的所占的百分比为30%;
(2)补全小组合作学习后学生学习兴趣的统计图;
(3)通过“小组合作学习”前后学生学习兴趣的对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?
分析 (1)用整体1减去极高、低、中所占的百分比,即可求出小组合作学习前学生学习兴趣为“高”的所占的百分比;
(2)用抽查的总人数减去学习兴趣极高、高和低的人数,求出学习兴趣“中”的人数,从而补全统计图;
(3)根据题意先分别求出小组合作学习后学习兴趣提高的人数,再用全校的总人数乘以学习兴趣获得提高的学生所占的百分比即可.
解答 解:(1)小组合作学习前学生学习兴趣为“高”的所占的百分比为1-25%-20%-25%=30%;
故答案为:30%;
(2)“小组合作学习”学习兴趣“中”的人数是100-30-35-5=30(人),补图如下: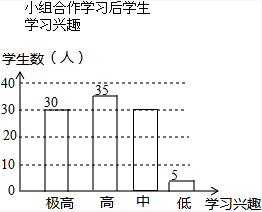
(3)小组合作学习前学生学习兴趣“中”的有100×25%=25(人),
小组合作学习后学习兴趣提高了30-25=5(人);
小组合作学习前学生学习兴趣“高”的有100×30%=30(人),
小组合作学习后学习兴趣提高了35-30=5(人);
小组合作学习前学生学习兴趣为“极高”的有100×25%=25(人),
小组合作学习后学习兴趣提高了30-25=5(人),
则2000×$\frac{5+5+5}{100}$=300(人).
答:全校2000名学生中学习兴趣获得提高的学生有300人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
6.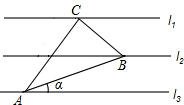 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,△ABC的三个顶点分别在这三条平行直线上,且∠ACB=90°,∠CAB=30°,则tanα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,△ABC的三个顶点分别在这三条平行直线上,且∠ACB=90°,∠CAB=30°,则tanα的值是( )
 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,△ABC的三个顶点分别在这三条平行直线上,且∠ACB=90°,∠CAB=30°,则tanα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,△ABC的三个顶点分别在这三条平行直线上,且∠ACB=90°,∠CAB=30°,则tanα的值是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{5}$ |




 如图所示,在平行四边形ABCD中,对角线AC与 BD相交于点O,M,N在对角线AC上,且AM=CN,求证:四边形BNDM是平行四边形.
如图所示,在平行四边形ABCD中,对角线AC与 BD相交于点O,M,N在对角线AC上,且AM=CN,求证:四边形BNDM是平行四边形.