题目内容
6.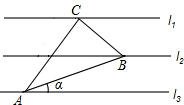 如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,△ABC的三个顶点分别在这三条平行直线上,且∠ACB=90°,∠CAB=30°,则tanα的值是( )
如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,△ABC的三个顶点分别在这三条平行直线上,且∠ACB=90°,∠CAB=30°,则tanα的值是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{5}$ |
分析 过点A作AD⊥l1于D,过点B作BE⊥l1于E,根据同角的余角相等求出∠CAD=∠BCE,然后证明△ACD和△CBE相似,列比例式求得CE,DE,得到AF,根据锐角的正切值等于对边比邻边求得结果.
解答  解:如图,过点A作AD⊥l1于D,过点B作BE⊥l1于E,反向延长EB交l3于F,设l1,l2,l3间的距离为1,
解:如图,过点A作AD⊥l1于D,过点B作BE⊥l1于E,反向延长EB交l3于F,设l1,l2,l3间的距离为1,
∵∠CAD+∠ACD=90°,
∠BCE+∠ACD=90°,
∴∠CAD=∠BCE,
∴△ACD∽△CEB,
∵∠CAB=30°,
∴$\frac{BC}{AC}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{BE}{CD}$=$\frac{CE}{AD}$=$\frac{BC}{AC}$=$\frac{\sqrt{3}}{3}$,
∴CD=$\sqrt{3}$,CE=$\frac{2\sqrt{3}}{3}$,
∴AF=$\frac{5\sqrt{3}}{3}$,
∴tanα=$\frac{BF}{AF}$=$\frac{\sqrt{3}}{5}$.
故选D.
点评 本题考查了全等三角形的判定与性质,直角三角形的性质,锐角三角函数的定义,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14. 一个正方体的表面展开图如图所示,则原正方体中字母“A”所在面的对面所标的字是( )
一个正方体的表面展开图如图所示,则原正方体中字母“A”所在面的对面所标的字是( )
 一个正方体的表面展开图如图所示,则原正方体中字母“A”所在面的对面所标的字是( )
一个正方体的表面展开图如图所示,则原正方体中字母“A”所在面的对面所标的字是( )| A. | 玉 | B. | 溪 | C. | 红 | D. | 塔 |
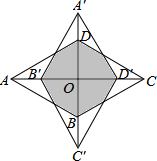 如图,菱形ABCD的一个内角是60°,将它绕对角线的交点O顺时针旋转90°后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为8$\sqrt{3}$-8,则菱形ABCD的边长为2.
如图,菱形ABCD的一个内角是60°,将它绕对角线的交点O顺时针旋转90°后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为8$\sqrt{3}$-8,则菱形ABCD的边长为2.