题目内容
13.先化简,再求值:(a+b)2-2a(b+1)-a2b÷b,其中a=$\frac{1}{2}$,b=-2.分析 先算乘法,再合并同类项,最后代入求出即可.
解答 解:原式=a2+2ab+b2-2ab-2a-a2
=b2-2a,
当$a=\frac{1}{2}$,b=-2时,原式=${(-2)^2}-2×\frac{1}{2}=3$.
点评 本题考查了整式的混合运算和求值的应用,能运用整式的运算法则进行化简是解此题的关键,难度适中.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
3.若实数x、y满足$\sqrt{2x-1}+$(y-1)2=0,则x+y的值等于( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
8.对于一个自然数n,如果能找到正整数x、y,使得n=x+y+xy,则称n为“好数”,例如:3=1+1+1×1,则3是一个“好数”,在8,9,10,11这四个数中,“好数”的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.计算$\frac{x-1}{x}$+$\frac{1}{x}$=( )
| A. | 1 | B. | $\frac{1}{x}$ | C. | $\frac{x+1}{x}$ | D. | $\frac{x-1}{x}$ |
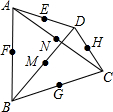 如图,四边形各边中点及对角线中点共六个点中,任取四个点连成四边形,最多可以有几个平行四边形?证明你的结论.
如图,四边形各边中点及对角线中点共六个点中,任取四个点连成四边形,最多可以有几个平行四边形?证明你的结论. 已知A(0,3),B(-4,0),C(-2,-3),D(4,-1),求图中四边形ABCD的面积.
已知A(0,3),B(-4,0),C(-2,-3),D(4,-1),求图中四边形ABCD的面积.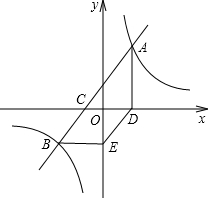 如图,直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.
如图,直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.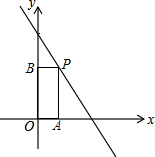 (1)如图,在一次函数y=-x+3的图象上取点P,作PA⊥x轴,作PB⊥y轴,垂足分别为A,B,且矩形OAPB的面积为2,则这样的点有A;
(1)如图,在一次函数y=-x+3的图象上取点P,作PA⊥x轴,作PB⊥y轴,垂足分别为A,B,且矩形OAPB的面积为2,则这样的点有A;