题目内容
18.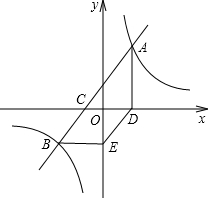 如图,直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.
如图,直线AB与x轴交于点C,与双曲线y=$\frac{k}{x}$交于A(3,$\frac{20}{3}$)、B(-5,a)两点,AD⊥x轴于点D,BE∥x轴且与y轴交于点E,判断四边形CBED的形状,并说明理由.
分析 由点C、D的坐标、已知条件“BE∥x轴”及两点间的距离公式求得,CD=5,BE=5,且BE∥CD,从而可以证明四边形CBED是平行四边形;然后在Rt△OED中根据勾股定理求得ED=5,所以ED=CD,从而证明四边形CBED是菱形.
解答 解:四边形CBED是菱形.
∵双曲线$y=\frac{k}{x}$过A(3,$\frac{20}{3}$),
∴k=20.
把B(-5,a)代入$y=\frac{20}{x}$,
得a=-4.
∴点B的坐标是(-5,-4).
∵AD⊥x轴于D,
∴D(3,0),
设直线AB的解析式为y=mx+n,将 A(3,$\frac{20}{3}$)、B(-5,-4)代入得:$\left\{{\begin{array}{l}{\frac{20}{3}=3m+n}\\{-4=-5m+n}\end{array}}\right.$
解得:$m=\frac{4}{3},n=\frac{8}{3}$.
∴直线AB的解析式为:$y=\frac{4}{3}x+\frac{8}{3}$.
∴点C的坐标是(-2,0).
∵BE∥x轴,∴点E的坐标是(0,-4).
而CD=5,BE=5,且BE∥CD.
∴四边形CBED是平行四边形.
在Rt△OED中,ED2=OE2+OD2,
∴ED=$\sqrt{{3^2}+{4^2}}$=5,
∴ED=CD.
∴□CBED是菱形.
点评 本题考查了反比例函数综合题及菱形的判定的知识.解答此题时,利用了反比例函数图象上点的坐标特征.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.在坐标平面上,点P在x轴的负半轴,且到原点的距离是6,则点P的坐标是( )
| A. | (0,6) | B. | (0.-6) | C. | (6,0) | D. | (-6,0) |
3.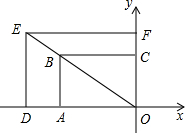 如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1:1.2,点B的坐标为(-3,2),则点E的坐标是( )
如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1:1.2,点B的坐标为(-3,2),则点E的坐标是( )
 如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1:1.2,点B的坐标为(-3,2),则点E的坐标是( )
如图,矩形OABC与矩形ODEF是位似图形,点O为位似中心,相似比为1:1.2,点B的坐标为(-3,2),则点E的坐标是( )| A. | (3.6,2.4) | B. | (-3,2.4) | C. | (-3.6,2) | D. | (-3.6,2.4) |
10.下面图形中既是轴对称图形,又是中心对称图形的是( )
| A. | 平行四边形 | B. | 等腰梯形 | C. | 正三角形 | D. | 菱形 |
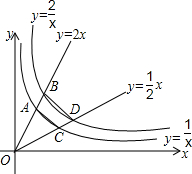 如图,直线y=2x、y=$\frac{1}{2}$x分别与双曲线y=$\frac{1}{x}$、y=$\frac{2}{x}$在第一象限的分支交于A、B、C、D四点,则四边形ABCD的面积为$\frac{3}{4}$.
如图,直线y=2x、y=$\frac{1}{2}$x分别与双曲线y=$\frac{1}{x}$、y=$\frac{2}{x}$在第一象限的分支交于A、B、C、D四点,则四边形ABCD的面积为$\frac{3}{4}$. 如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=8,AO=6,则四边形DEFG的周长为( )
如图,△ABC的中线BD、CE交于点O,连接OA,点G、F分别为OC、OB的中点,BC=8,AO=6,则四边形DEFG的周长为( ) 超速行驶是引发交通事故的主要原因之一,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,距离大路(BC)为30米,一辆小轿车由西向东匀速行驶,测得此车从B处到C处所用的时间为5秒,∠BAC=60°.
超速行驶是引发交通事故的主要原因之一,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在A处,距离大路(BC)为30米,一辆小轿车由西向东匀速行驶,测得此车从B处到C处所用的时间为5秒,∠BAC=60°.