题目内容
4.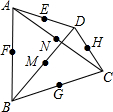 如图,四边形各边中点及对角线中点共六个点中,任取四个点连成四边形,最多可以有几个平行四边形?证明你的结论.
如图,四边形各边中点及对角线中点共六个点中,任取四个点连成四边形,最多可以有几个平行四边形?证明你的结论.
分析 在四边形ABCD中,由F,G,H,E分别是AB,BC,CD,DA的中点,根据三角形中位线定理可得FG∥AC,EH∥AC;FG=$\frac{1}{2}$AC,EH=$\frac{1}{2}$AC,那么FG∥EH,FG=EH,根据有一组对边平行且相等的四边形是平行四边形得到四边形FGHE是平行四边形;同理可得四边形MGNE与四边形FMHN都是平行四边形;即最多可以有3个平行四边形.
解答 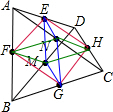 解:最多可以有3个平行四边形,即?FGHE;?MGNE;?FMHN.利用如下:
解:最多可以有3个平行四边形,即?FGHE;?MGNE;?FMHN.利用如下:
∵在四边形ABCD中,F,G,H,E分别是AB,BC,CD,DA的中点,
∴FG∥AC,EH∥AC;FG=$\frac{1}{2}$AC,EH=$\frac{1}{2}$AC,
∴FG∥EH,FG=EH,
∴四边形FGHE是平行四边形;
∵在四边形ABCD中G,E,M,N分别是BC,DA,BD,AC的中点,
∴MG∥CD,EN∥CD,MG=$\frac{1}{2}$CD,EN=$\frac{1}{2}$CD,
∴MG∥EN,MG=EN,
∴四边形MGNE是平行四边形;
∵在四边形ABCD中F,H,M,N分别是AB,CD,BD,AC的中点,
∴FM∥AD,NH∥AD;FM=$\frac{1}{2}$AD,NH=$\frac{1}{2}$AD,
∴FM∥NH;FM=NH,
∴四边形FMHN是平行四边形,
∴最多可以有3个平行四边形.
点评 本题考查了三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.也考查了平行四边形的判定.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
16.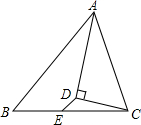 已知△ABC中,AB=6,AC=5,从点C向∠A的平分线作垂线,垂足为D,E为BC中点,则DE的长是( )
已知△ABC中,AB=6,AC=5,从点C向∠A的平分线作垂线,垂足为D,E为BC中点,则DE的长是( )
 已知△ABC中,AB=6,AC=5,从点C向∠A的平分线作垂线,垂足为D,E为BC中点,则DE的长是( )
已知△ABC中,AB=6,AC=5,从点C向∠A的平分线作垂线,垂足为D,E为BC中点,则DE的长是( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
14.下列运算正确的是( )
| A. | 2(a+b)=2a+b | B. | (a-b)2=a2-b2 | C. | a5÷a3=a2 | D. | a2b+ab2=a3b3 |
 如图,点A(1,0)第一次跳动至点A1(-1,1),第二次跳动至点A2(2,1),第三次跳动至点A3(-2,2),第四次跳动至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是(51,50).
如图,点A(1,0)第一次跳动至点A1(-1,1),第二次跳动至点A2(2,1),第三次跳动至点A3(-2,2),第四次跳动至点A4(3,2),…,依此规律跳动下去,点A第100次跳动至点A100的坐标是(51,50). 如图,四边形ABCD是菱形,过点A、C作对角线AC的垂线,分别交CD和AB的延长线于点E、F.已知AE=2,四边形AECF的周长为12,则菱形的边长为( )
如图,四边形ABCD是菱形,过点A、C作对角线AC的垂线,分别交CD和AB的延长线于点E、F.已知AE=2,四边形AECF的周长为12,则菱形的边长为( )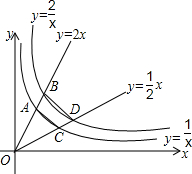 如图,直线y=2x、y=$\frac{1}{2}$x分别与双曲线y=$\frac{1}{x}$、y=$\frac{2}{x}$在第一象限的分支交于A、B、C、D四点,则四边形ABCD的面积为$\frac{3}{4}$.
如图,直线y=2x、y=$\frac{1}{2}$x分别与双曲线y=$\frac{1}{x}$、y=$\frac{2}{x}$在第一象限的分支交于A、B、C、D四点,则四边形ABCD的面积为$\frac{3}{4}$.