题目内容
 如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE.
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE.考点:全等三角形的判定与性质,平行线的判定
专题:证明题
分析:欲证明AB∥DE,只需证得∠B=∠FED.由Rt△ABC≌Rt△DEF,根据全等三角形的性质推知该结论即可.
解答: 证明:如图,∵FB=CE,
证明:如图,∵FB=CE,
∴FB+FC=CE+FC,即BC=EF.
又∵∠A=∠D=90°,
在Rt△ABC与Rt△DEF中,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠B=∠FED,
∴AB∥DE.
 证明:如图,∵FB=CE,
证明:如图,∵FB=CE,∴FB+FC=CE+FC,即BC=EF.
又∵∠A=∠D=90°,
在Rt△ABC与Rt△DEF中,
|
∴Rt△ABC≌Rt△DEF(HL),
∴∠B=∠FED,
∴AB∥DE.
点评:本题主要考查两直线平行的性质,两直线平行的判定定理的熟练应用,要证明AB∥DE,就得先找出判定的条件,如∠B=∠FED.

练习册系列答案
相关题目
在△ABC中,O为内心,∠A=70°,则∠BOC=( )
| A、140° | B、135° |
| C、130° | D、125° |
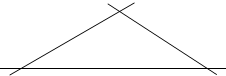 如图,有三条交叉的公路,现要在三条公路交叉所形成的区域内建一货运站,使得货运站到三条公路的路程一样长,请问如何确定货运站的位置?(保留作图痕迹) 简单叙述你的方法.
如图,有三条交叉的公路,现要在三条公路交叉所形成的区域内建一货运站,使得货运站到三条公路的路程一样长,请问如何确定货运站的位置?(保留作图痕迹) 简单叙述你的方法.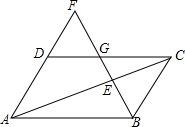 如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.
如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE. 已知:如图,AB=EF,BC=FD,AD=EC,求证:∠B=∠F.
已知:如图,AB=EF,BC=FD,AD=EC,求证:∠B=∠F. 如图,∠XOY内有一点P,试在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.写出你作图的主要步骤,并标明你所确定的点(要求画出草图,保留作图痕迹).
如图,∠XOY内有一点P,试在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.写出你作图的主要步骤,并标明你所确定的点(要求画出草图,保留作图痕迹).