题目内容
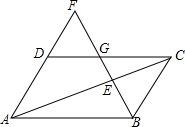 如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.
如图,F为平行四边形ABCD的边AD的延长线上的一点,BF分别交于CD、AC于G、E,若EF=32,GE=8,求BE.考点:平行线分线段成比例
专题:
分析:利用平行四边形的性质得出相似三角形,进而利用相似三角形的性质得出答案.
解答: 解:设BE=x,
解:设BE=x,
∵EF=32,GE=8,
∴FG=32-8=24,
∵AD∥BC,
∴△AFE∽△CBE,
∴
=
,
∴则
=
=
+1①
∵DG∥AB,
∴△DFG∽△CBG,
∴
=
代入①
=
+1,
解得:x=±16(负数舍去),
故BE=16.
 解:设BE=x,
解:设BE=x,∵EF=32,GE=8,
∴FG=32-8=24,
∵AD∥BC,
∴△AFE∽△CBE,
∴
| EF |
| EB |
| AF |
| BC |
∴则
| 32 |
| x |
| DF+AD |
| BC |
| DF |
| BC |
∵DG∥AB,
∴△DFG∽△CBG,
∴
| DF |
| BC |
| 24 |
| 8+x |
| 32 |
| x |
| 24 |
| 8+x |
解得:x=±16(负数舍去),
故BE=16.
点评:此题主要考查了相似三角形的判定与性质以及平行四边形的性质,得出△DFG∽△CBG是解题关键.

练习册系列答案
相关题目
 如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠1=∠2;④△ACN≌△ABM.其中正确的有( )
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠1=∠2;④△ACN≌△ABM.其中正确的有( ) 如图,AD为△ABC的中线,分别过点C、B作AD的垂线,垂足分别为E、F.求证:BF=CE.
如图,AD为△ABC的中线,分别过点C、B作AD的垂线,垂足分别为E、F.求证:BF=CE.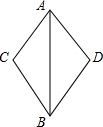 已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD.
已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD.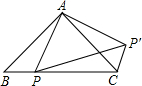 如图,△ABC是等腰直角三角形,点P是斜边BC上一点,且AB=4,BP=2,先将△ABP绕点A逆时针旋转后,能与△ACP′重合,则∠BCP′=
如图,△ABC是等腰直角三角形,点P是斜边BC上一点,且AB=4,BP=2,先将△ABP绕点A逆时针旋转后,能与△ACP′重合,则∠BCP′= 如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE.
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE. 如图,∠ABC=∠DCB=90°,E,F为BC上两点,且BE=CF,AB=DC.求证:△ABF≌△DCE.
如图,∠ABC=∠DCB=90°,E,F为BC上两点,且BE=CF,AB=DC.求证:△ABF≌△DCE.