题目内容
在△ABC中,O为内心,∠A=70°,则∠BOC=( )
| A、140° | B、135° |
| C、130° | D、125° |
考点:三角形的内切圆与内心
专题:
分析:根据三角形的内角和定理求出∠ABC+∠ACB的度数,根据三角形的内心,求出∠OBC+∠OCB=
(∠ABC+∠ACB),代入求出∠OBC+∠OCB,根据三角形的内角和定理求出∠BOC即可.
| 1 |
| 2 |
解答:解:∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°,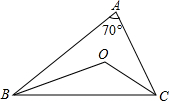
∵点O是△ABC的内心,
∴∠OBC=
∠ABC,∠OCB=
∠ACB,
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
故选D.
∴∠ABC+∠ACB=180°-∠A=110°,

∵点O是△ABC的内心,
∴∠OBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠OBC+∠OCB=
| 1 |
| 2 |
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
故选D.
点评:本题考查了三角形的内角和定理,三角形的内心,角平分线定义等知识点的应用,关键是求出∠OBC+∠OCB的度数,题目比较典型,主要训练了学生的推理能力和计算能力.

练习册系列答案
相关题目
 向阳小区计划在一块正方形土地上建一座花坛,园艺师设计了4种不同的图案(如图所示),其中阴影部分用于种植月季花.哪种方案种植月季花的面积最大?
向阳小区计划在一块正方形土地上建一座花坛,园艺师设计了4种不同的图案(如图所示),其中阴影部分用于种植月季花.哪种方案种植月季花的面积最大? 如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠1=∠2;④△ACN≌△ABM.其中正确的有( )
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠1=∠2;④△ACN≌△ABM.其中正确的有( ) 如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是
如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B.已知∠A=30°,则∠C的大小是 如图,AD为△ABC的中线,分别过点C、B作AD的垂线,垂足分别为E、F.求证:BF=CE.
如图,AD为△ABC的中线,分别过点C、B作AD的垂线,垂足分别为E、F.求证:BF=CE.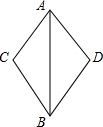 已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD.
已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD. 如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE.
如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.∠A=∠D=90°;求证:AB∥DE. 如图所示:正方形网格中的四边形ABCD,若小方格的边长为1,则四边形ABCD的面积是
如图所示:正方形网格中的四边形ABCD,若小方格的边长为1,则四边形ABCD的面积是