题目内容
20.如图,?ABCD中,∠DAB=120°,设对角线AC、BD交于点O,过点O作OF⊥AC交∠ABC外角的平分线于点F,OF与BC交于E点(1)如图1,求证:BC-AB=BF;
(2)如图2,在(1)的条件下,若AD=3,BF=1,求CE的长.
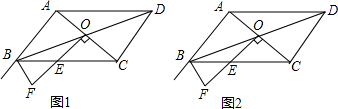
分析 (1)如图1中,连接FA、FC,作FN⊥BC、FM⊥AB垂足分别为N、M,先证明△FNC≌△FMA,△FBN≌△FBM,得AM=CN,BM=BN,再证明BF=2BM,BC-AB=2BM即可解决问题.
(2)如图2中,作AH⊥BC于H,30°性质求出BH、AH,利用勾股定理求出AC,再利用△ECO≌△ACH,得$\frac{OC}{CH}$=$\frac{CE}{CA}$即可解决问题.
解答 (1)证明:如图1中,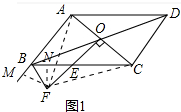 连接FA、FC,作FN⊥BC、FM⊥AB垂足分别为N、M.
连接FA、FC,作FN⊥BC、FM⊥AB垂足分别为N、M.
∵四边形ABCD是平行四边形,
∴AD∥BC,AO=OC,
∵FO⊥AC,∠BAD=120°,
∴FA=FC,∠MBC=∠BAD=120°,
∵BF平分∠CBM,FM⊥AB,FN⊥BC,
∴FM=FN,∠FBM=∠FBN=60°,
在RT△FNC和RT△FMA中,
$\left\{\begin{array}{l}{FC=FA}\\{FN=FM}\end{array}\right.$,
∴△FNC≌△FMA,
∴AM=NC,
在RT△FBN和RT△FBM中,
$\left\{\begin{array}{l}{FB=FB}\\{FM=FN}\end{array}\right.$,
∴△FBN≌△FBM,
∴BM=BN,
∴BC-AB=(BN+NC)-(AM-BN)=2BM,
在RT△BMF中,∵∠FMB=90°,∠MFB=30°,
∴BF=2BM,
∴BC-AB=BF.
(2)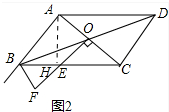 如图2中,作AH⊥BC于H.
如图2中,作AH⊥BC于H.
在RT△∵∠AHB=90°,AB=2,∠ABC=60°,
∴BE=1,AE=$\sqrt{3}$,HC=BC-BH=3-1=2,
∴AC=$\sqrt{A{H}^{2}+H{C}^{2}}$=$\sqrt{7}$,
∴OC=$\frac{1}{2}$AC=$\frac{\sqrt{7}}{2}$,
∵∠ECO=∠ACH,∠EOC=∠AHC=90°,
∴△ECO≌△ACH,
∴$\frac{OC}{CH}$=$\frac{CE}{CA}$,
∴$\frac{\frac{\sqrt{7}}{2}}{2}$=$\frac{CE}{\sqrt{7}}$,
∴CE=$\frac{7}{4}$.
点评 本题考查平行四边形的性质、全等三角形的判定和性质、角平分线的性质定理、勾股定理.直角三角形30度角的性质等知识,解题的关键是添加辅助线构造全等三角形,学会常用辅助线的添加方法,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案| A. | 1或4 | B. | 1或-4 | C. | -1或-4 | D. | -1或4 |
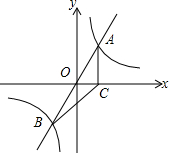 如图,直线y=mx与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC.
如图,直线y=mx与双曲线y=$\frac{k}{x}$相交于A、B两点,A点的坐标为(1,2),AC⊥x轴于C,连结BC. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论:
如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下面四个结论: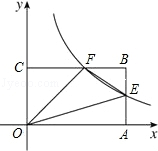 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则:
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边长AB、BC分别交于点E、F,已知S△FOC=3 且AE=BE,则: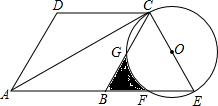 如图:已知菱形ABCD,∠DAB=60°,延长AB到点E,使BE=AB,以CE为直径作⊙O,交BC、BE于点G、F.
如图:已知菱形ABCD,∠DAB=60°,延长AB到点E,使BE=AB,以CE为直径作⊙O,交BC、BE于点G、F.