题目内容
 如图,在△ABC中,D是BC的垂直平分线DH上一点,DF⊥AB于F,DE⊥AC交AC的延长线于E,且BF=CE.
如图,在△ABC中,D是BC的垂直平分线DH上一点,DF⊥AB于F,DE⊥AC交AC的延长线于E,且BF=CE.(1)求证:AD平分∠BAC;
(2)若∠BAC=80°,求∠DCB的度数.
考点:全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质
专题:
分析:(1)连接BD,根据线段垂直平分线上的点到两端点的距离相等可得BD=CD,再利用“HL”证明Rt△BDF和Rt△CDE全等,根据全等三角形对应边相等可得DE=DF,然后根据到角的两边距离相等的点在角的平分线上证明;
(2)根据全等三角形对应角相等可得∠CDE=∠BDF,求出∠BDC=∠EDF,再根据四边形的内角和定理求出∠EDF,然后根据等腰三角形两底角相等列式计算即可得解.
(2)根据全等三角形对应角相等可得∠CDE=∠BDF,求出∠BDC=∠EDF,再根据四边形的内角和定理求出∠EDF,然后根据等腰三角形两底角相等列式计算即可得解.
解答: (1)证明:如图,连接BD,
(1)证明:如图,连接BD,
∵DH垂直平分BC,
∴BD=CD,
在Rt△BDF和Rt△CDE中,
,
∴Rt△BDF≌Rt△CDE(HL),
∴DE=DF,
∵DF⊥AB于F,DE⊥AC,
∴AD平分∠BAC;
(2)解:∵Rt△BDF≌Rt△CDE,
∴∠CDE=∠BDF,
∴∠BDC=∠EDF,
∵∠BAC=80°,
∴∠EDF=360°-90°×2-80°=100°,
∴∠BDC=100°,
∵BD=CD,
∴∠DCB=
(180°-100°)=50°.
 (1)证明:如图,连接BD,
(1)证明:如图,连接BD,∵DH垂直平分BC,
∴BD=CD,
在Rt△BDF和Rt△CDE中,
|
∴Rt△BDF≌Rt△CDE(HL),
∴DE=DF,
∵DF⊥AB于F,DE⊥AC,
∴AD平分∠BAC;
(2)解:∵Rt△BDF≌Rt△CDE,
∴∠CDE=∠BDF,
∴∠BDC=∠EDF,
∵∠BAC=80°,
∴∠EDF=360°-90°×2-80°=100°,
∴∠BDC=100°,
∵BD=CD,
∴∠DCB=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定与性质,线段垂直平分线上的点到两端点的距离相等的性质,等腰三角形的性质,熟记各性质是解题的关键,难点在于(2)求出∠BDC=∠EDF.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
下列命题的逆命题不成立的是( )
| A、两条直线平行,同旁内角互补 |
| B、若两个数的绝对值相等,则这两个数的相等 |
| C、对顶角相等 |
| D、如果a=b或a+b=0,b2=a2 |
 认真阅读并填空.
认真阅读并填空.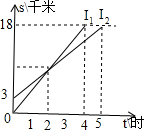 小李家、小于家、学校在同一条路线上,小李和小于分别从家同时出发到学校,如图l1,l2分别表示小李和小于前往学校所走的路程s/千米与所用的时间t/时的关系.
小李家、小于家、学校在同一条路线上,小李和小于分别从家同时出发到学校,如图l1,l2分别表示小李和小于前往学校所走的路程s/千米与所用的时间t/时的关系. 如图,平面上有四个点A、B、C、D,根据下列语句画图.
如图,平面上有四个点A、B、C、D,根据下列语句画图.