题目内容
如图,在平面直角坐标系xOy中,△OAB如图放置,点P是AB边上的一点,过点P的反比例函数y=
(k>0,x>0)与OA边交于点E,连接OP.
(1)如图1,若点A的坐标为(3,4),点B的坐标为(5,0),且△OPB的面积为5,求直线AB和反比例函数的解析式;
(2)如图2,若∠AOB=60°,过P作PC∥OA,与OB交于点C,若PC=
OE,并且△OPC的面积为
,求OE的长.
(3)在(2)的条件下,过点P作PQ∥OB,交OA于点Q,点M是直线PQ上的一个动点,若△OEM是以OE为直角边的直角三角形,则点M的坐标为 .

| k |
| x |
(1)如图1,若点A的坐标为(3,4),点B的坐标为(5,0),且△OPB的面积为5,求直线AB和反比例函数的解析式;
(2)如图2,若∠AOB=60°,过P作PC∥OA,与OB交于点C,若PC=
| 1 |
| 2 |
3
| ||
| 2 |
(3)在(2)的条件下,过点P作PQ∥OB,交OA于点Q,点M是直线PQ上的一个动点,若△OEM是以OE为直角边的直角三角形,则点M的坐标为

考点:反比例函数综合题
专题:
分析:(1)过点P作PD⊥OB于点D,根据点B的坐标为(5,0),且△OPB的面积为
求出PD的长,求出直线AB的解析式,故可得出P点坐标,利用待定系数法求出反比例函数的解析式即可;
(2)先根据勾股定理求出OA的长,△OPC的面积为
求出OC的长,再由PC∥OA可知△BCP∽△BOA,故可得出OC的长,由PC=
OE即可得出OE的长.
(3)先求得E的坐标,然后根据直线OA求得OM或EM的解析式,把y=1代入解析式即可求得M的坐标;
| 5 |
| 2 |
(2)先根据勾股定理求出OA的长,△OPC的面积为
3
| ||
| 2 |
| 1 |
| 2 |
(3)先求得E的坐标,然后根据直线OA求得OM或EM的解析式,把y=1代入解析式即可求得M的坐标;
解答: 解:(1)过点P作PD⊥OB于点D,
解:(1)过点P作PD⊥OB于点D,
∵点B的坐标为(5,0),
△OPB的面积为
,
∴
×5PD=
,解得PD=1,
设直线AB的解析式为
y=ax+b(a≠0),
∵A(3,4),B(5,0),
∴
,解得
,
∴直线AB的解析式为y=-2x+10,
当y=1时,-2x+10=1,解得x=
,
∴P(
,1),
∵点P的反比例函数y=
(x>0)上,
∴1=
,解得k=
,
∴反比例函数的解析式为:y=
;
(2)∵点A的坐标为(3,4),
∴OA=
=5,
∵△OPC的面积为
,
∴
OC×1=
,解得OC=3
,
∴BC=5-3
,
∵PC∥OA,
∴△BCP∽△BOA,
∴
=
,即
=
,解得PC=5-3
,
∵PC=
OE,
∴OE=10-6
.
(3)∵点A的坐标为(3,4),
∴直线OA为:y=
x,
∵反比例函数的解析式为:y=
;
∴E(
,
),
当∠EOM=90°时,直线OM为:y=-
x,
∵P(
,1),
∴1=-
x,解得x=-
,
∴M(-
,1),
当∠OEM=90°时,直线EM为:y=-
x+b,
∵E(
,
),
∴
=-
×
+b,解得:b=2
,
∴直线EM为y=-
x+2
,
∵P(
,1),
∴1=-
x+2
,解得:x=
,
∴M(
,1)
∴M的坐标为(-
,1)或(
,1);
 解:(1)过点P作PD⊥OB于点D,
解:(1)过点P作PD⊥OB于点D,∵点B的坐标为(5,0),
△OPB的面积为
| 5 |
| 2 |
∴
| 1 |
| 2 |
| 5 |
| 2 |
设直线AB的解析式为
y=ax+b(a≠0),
∵A(3,4),B(5,0),
∴
|
|
∴直线AB的解析式为y=-2x+10,
当y=1时,-2x+10=1,解得x=
| 9 |
| 2 |
∴P(
| 9 |
| 2 |
∵点P的反比例函数y=
| k |
| x |
∴1=
| k | ||
|
| 9 |
| 2 |
∴反比例函数的解析式为:y=
| 9 |
| 2x |
(2)∵点A的坐标为(3,4),
∴OA=
| 32+42 |
∵△OPC的面积为
| 3 |
| 2 |
| 3 |
∴
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
∴BC=5-3
| 3 |
∵PC∥OA,
∴△BCP∽△BOA,
∴
| PC |
| OA |
| BC |
| OB |
| PC |
| 5 |
5-3
| ||
| 5 |
| 3 |
∵PC=
| 1 |
| 2 |
∴OE=10-6
| 3 |
(3)∵点A的坐标为(3,4),
∴直线OA为:y=
| 4 |
| 3 |
∵反比例函数的解析式为:y=
| 9 |
| 2x |
∴E(
3
| ||
| 4 |
| 6 |
当∠EOM=90°时,直线OM为:y=-
| 3 |
| 4 |
∵P(
| 9 |
| 2 |
∴1=-
| 3 |
| 4 |
| 4 |
| 3 |
∴M(-
| 4 |
| 3 |
当∠OEM=90°时,直线EM为:y=-
| 3 |
| 4 |
∵E(
3
| ||
| 4 |
| 6 |
∴
| 6 |
| 3 |
| 4 |
3
| ||
| 4 |
| 6 |
∴直线EM为y=-
| 3 |
| 4 |
| 6 |
∵P(
| 9 |
| 2 |
∴1=-
| 3 |
| 4 |
| 6 |
8
| ||
| 3 |
∴M(
8
| ||
| 3 |
∴M的坐标为(-
| 4 |
| 3 |
8
| ||
| 3 |
点评:本题考查的是反比例函数综合题,涉及到用待定系数法求一次函数及反比例函数的解析式、相似三角形的判定与性质等知识,难度适中.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图,在△ABC中,D是BC的垂直平分线DH上一点,DF⊥AB于F,DE⊥AC交AC的延长线于E,且BF=CE.
如图,在△ABC中,D是BC的垂直平分线DH上一点,DF⊥AB于F,DE⊥AC交AC的延长线于E,且BF=CE. 如图,四边形ABCD是平行四边形,∠ABC=70°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F,则∠1的度数为
如图,四边形ABCD是平行四边形,∠ABC=70°,BE平分∠ABC且交AD于点E,DF∥BE且交BC于点F,则∠1的度数为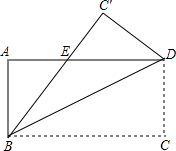 如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为
如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为 如图,是一张正方形跳舞毯,每个方格除了图案外都相同,那么小轩的右脚尖(视为一个点)自由、随机地踩到画有“
如图,是一张正方形跳舞毯,每个方格除了图案外都相同,那么小轩的右脚尖(视为一个点)自由、随机地踩到画有“ ”正方形(包含边界)的概率是
”正方形(包含边界)的概率是