题目内容
11.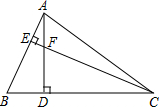 如图,△ABC的两条高AD、CE相交于点,F,CF=AB:
如图,△ABC的两条高AD、CE相交于点,F,CF=AB:(1)求证:△ABD≌△CDF;
(2)若∠BCE=20°,求∠BAC度数.
分析 (1)由∠ADB=∠CDF=∠CEB=90°,推出∠B+∠BCE=90°,∠B+∠BAD=90°,推出∠BAD=∠DCF,根据AAS即可证明;
(2)由△CDF≌△ABD.推出AD=CD,∠DCF=∠BAD=20°,由∠ADC=90°,推出∠DAC=45°,由此即可解决问题;
解答 (1)证明:∵AD、CE是高,
∴∠ADB=∠CDF=∠CEB=90°,
∴∠B+∠BCE=90°,∠B+∠BAD=90°,
∴∠BAD=∠DCF,
在△CDF和△ADB中,
$\left\{\begin{array}{l}{∠DCF=∠BAD}\\{∠CDF=∠ADB}\\{CF=AB}\end{array}\right.$,
∴△CDF≌△ABD.
(2)∵△CDF≌△ABD.
∴AD=CD,∠DCF=∠BAD=20°,
∵∠ADC=90°,
∴∠DAC=45°,
∴∠BAC=∠BAD+∠DAC=65°.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的判定和性质等知识,解题的关键是正确寻找全等三角形全等的条件,属于中考常考题型.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
11.下列各组二次根式化简后,被开方数不相同的一组是( )
| A. | $\sqrt{0.3}$和$\sqrt{0.03}$ | B. | $\sqrt{\frac{2}{3}}$和$\sqrt{54}$ | C. | $\sqrt{12}$和$\sqrt{0.75}$ | D. | $\sqrt{\frac{4}{5}}$和$\sqrt{{2}^{2}+{4}^{2}}$ |
12.判断下列几组数据中,不可以作为三角形的三条边的是( )
| A. | 6,10,17 | B. | 7,12,15 | C. | 13,15,20 | D. | 7,24,25 |
3.下列代数式是最简形式的是( )
| A. | $\frac{{{x^2}-4}}{x-2}$ | B. | $\frac{{4{x^2}+4x+1}}{2x+1}$ | C. | $\sqrt{4{x^3}}$ | D. | $\frac{{\sqrt{5}-1}}{2}$ |
 BD平分∠ABC,CD平分外角∠ACG,DE∥BC交AB于E,交AC于F,线段EF与BE、CF有什么关系?
BD平分∠ABC,CD平分外角∠ACG,DE∥BC交AB于E,交AC于F,线段EF与BE、CF有什么关系?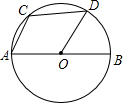 如图,已知AB是⊙O的直径,弦AC与半径OD平行.
如图,已知AB是⊙O的直径,弦AC与半径OD平行.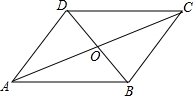 己知如图,在平行四边形ABCD中,AC=$\sqrt{2}$AB,求证:△AOB∽△ABC.
己知如图,在平行四边形ABCD中,AC=$\sqrt{2}$AB,求证:△AOB∽△ABC.