题目内容
4.已知α为锐角,且3sinα-2cosα=1,则tanα=$\frac{3+\sqrt{3}}{4}$,$\frac{3-\sqrt{3}}{4}$.分析 根据锐角三角函数的关系,可得关于tanα的方程,根据解方程,可得答案.
解答 解:如图: ,
,
由锐角三角函数的关系,得sinα=$\frac{a}{c}$,cosα=$\frac{b}{c}$,tanα=$\frac{a}{b}$,a2+b2=c2.
由3sinα-2cosα=1,得$\frac{3a}{c}$-$\frac{2b}{c}$=1.
两边都乘以c,得3a-2b=c.
(3a-2b)2=a2+b2.
化简,得
8a2-12ab+3b2=0.
两边都除以ab,得
8$\frac{a}{b}$-12+3$\frac{b}{a}$=0.
即8tanα-12+$\frac{3}{tanα}$=0.
8tan2α-12tanα+3=0.
解得tanα=$\frac{3+\sqrt{3}}{4}$,tanα=$\frac{3-\sqrt{3}}{4}$,
故答案为:$\frac{3+\sqrt{3}}{4}$,$\frac{3-\sqrt{3}}{4}$.
点评 本题考查了锐角三角函数,利用锐角三角函数的关系得出关于tanα的方程是解题关键.

练习册系列答案
相关题目

 已知:AB∥CD,求∠B、∠D、∠P的关系.
已知:AB∥CD,求∠B、∠D、∠P的关系. 学校的生物老师想利用一边长为15米的墙及可以围成24米长的建筑材料,建造一间“小动物之家”,如图所示,它的平面图是长方形,请你帮老师计算一下,小动物之家的面积能否为32平方米.
学校的生物老师想利用一边长为15米的墙及可以围成24米长的建筑材料,建造一间“小动物之家”,如图所示,它的平面图是长方形,请你帮老师计算一下,小动物之家的面积能否为32平方米.
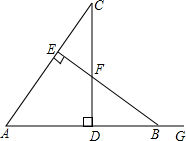 如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=20°,AB=10,AD=6,G为AB延长线上一点,求∠EBG的度数和CE的长.
如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=20°,AB=10,AD=6,G为AB延长线上一点,求∠EBG的度数和CE的长. 如图,已知∠1+∠2=80°,则∠3=140°.
如图,已知∠1+∠2=80°,则∠3=140°.