题目内容
16．计算$\sqrt{16}$×$\sqrt{\frac{1}{2}}$+$\sqrt{2}$×$\sqrt{8}$的结果估计在（ ）| A． | 6至7之间 | B． | 7至8之间 | C． | 8至9之间 | D． | 9至10之间 |
分析 先根据二次根式的乘法计算得到原式=$\sqrt{8}$+4，由于4＜8＜9，则2＜$\sqrt{8}$＜3，于是有6＜$\sqrt{8}$+4＜7．
解答 解：原式=$\sqrt{16×\frac{1}{2}}$+$\sqrt{2×8}$=$\sqrt{8}$+4，
∵4＜8＜9，
∴2＜$\sqrt{8}$＜3，
∴6＜$\sqrt{8}$+4＜7．
故选A．
点评 本题考查了二次根式的混合运算：先把各二次根式化为最简二次根式，在进行二次根式的乘除运算，然后合并同类二次根式．也考查了估算无理数的大小．
练习册系列答案
名校课堂系列答案
相关题目
6．下列方程中，关于x的一元二次方程的是（ ）
| A． | x2$+\frac{1}{{x}^{2}}=0$ | B． | ax2+bx+c=0 | C． | （x-1）（x+2）=1 | D． | x（x-1）=x2+2x |
11．下列实数-$\sqrt{2}$，$\frac{π}{2}$，$\frac{22}{7}$，0.1414，$\root{3}{9}$，$\sqrt{11}$，0.2002000200002中，无理数的个数是（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
1．已知$\sqrt{x+3}$+|y-2|=0，那么x+y的值是（ ）
| A． | 1 | B． | -1 | C． | -3 | D． | 2 |
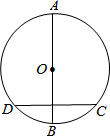如图⊙O，AB是它的直径，DC是它上面的一条弦，已知DC=6，AB⊥DC，圆心O到DC的距离为4，则圆的半径是（ ）
小芳从正面（图示“主视方向”）观察如图的热水瓶时，得到的主视图是（ ）
