题目内容
2．
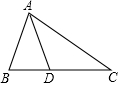已知：如图，在△ABC中，AD是它的角平分线，AB=6cm，AC=8cm，则 S△ABD：S△ACD=（ ）| A． | 4：3 | B． | 3：4 | C． | 16：9 | D． | 9：16 |
分析 作DE⊥AB于E，DF⊥AC于F，根据角平分线的性质得到DE=DF，根据三角形的面积公式计算即可．
解答 解：
作DE⊥AB于E，DF⊥AC于F，
∵AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE=DF，
∴S△ABD：S△ACD=$\frac{1}{2}$×AB×DE：$\frac{1}{2}$×AC×DF=AB：AC=3：4，
故选：B．
点评 本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
练习册系列答案
相关题目
13．
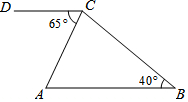如图，△ABC中，∠B=40°，过点C作CD∥AB，∠ACD=65°，则∠ACB的度数为（ ）
如图，△ABC中，∠B=40°，过点C作CD∥AB，∠ACD=65°，则∠ACB的度数为（ ）| A． | 105° | B． | 95° | C． | 85° | D． | 75° |
10．下列调查中，适宜采用全面调查（普查）方式的是（ ）
| A． | 调查市场上饮用水的质量情况 | |
| B． | 调查某品牌圆珠笔芯的使用寿命 | |
| C． | 调查乘坐飞机的旅客是否携带了危禁物品 | |
| D． | 调查我市市民每天的上网时长 |
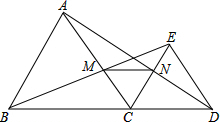如图，△ABC与△CDE都是等边三角形，B，C，D在一条直线上，连结B，E两点交AC于点M，连结A，D两点交CE于N点．
如图，AC=BD，AC⊥BC于C，BD⊥AD于D，AC与BD交于点E．有下列结论：①△ABC≌△BAD；②△ADE≌△BCE；③点E在线段AB的垂直平分线上．以上结论正确的有（ ）