题目内容
6.阅读下面计算过程:$\frac{1}{\sqrt{2}+1}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}$-1;
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}$-$\sqrt{2}$;
$\frac{1}{\sqrt{5}+2}$=$\frac{1×(\sqrt{5}-2)}{(\sqrt{5}+2)(\sqrt{5}-2)}$=$\sqrt{5}$-2.
试求:(1)$\frac{1}{\sqrt{7}+\sqrt{6}}$=$\sqrt{7}$-$\sqrt{6}$.
(2)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$(n为正整数)=$\sqrt{n+1}$-$\sqrt{n}$.
(3)$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{398}+\sqrt{399}}$+$\frac{1}{\sqrt{399}+\sqrt{400}}$的值.
分析 (1)先找出有理化因式,最后求出即可;
(2)先找出有理化因式,最后求出即可;
(3)先分母有理化,再合并即可.
解答 解:(1)$\frac{1}{\sqrt{7}+\sqrt{6}}$=$\frac{\sqrt{7}-\sqrt{6}}{(\sqrt{7}+\sqrt{6})×(\sqrt{7}-\sqrt{6})}$=$\sqrt{7}$-$\sqrt{6}$,
故答案为:$\sqrt{7}$-$\sqrt{6}$;
(2)原式=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})×(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}$-$\sqrt{n}$,
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(3)原式=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)×(\sqrt{2}-1)}$+$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})×(\sqrt{3}-\sqrt{2})}$+…+$\frac{1×(\sqrt{400}-\sqrt{399})}{(\sqrt{400}+\sqrt{399})×(\sqrt{400}-\sqrt{399})}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{400}$-$\sqrt{399}$
=$\sqrt{400}$-1
=19.
点评 本题考查了分母有理化,能正确分母有理化是解此题的关键.

练习册系列答案
相关题目
11. 如图,AC=BD,AC⊥BC于C,BD⊥AD于D,AC与BD交于点E.有下列结论:①△ABC≌△BAD;②△ADE≌△BCE;③点E在线段AB的垂直平分线上.以上结论正确的有( )
如图,AC=BD,AC⊥BC于C,BD⊥AD于D,AC与BD交于点E.有下列结论:①△ABC≌△BAD;②△ADE≌△BCE;③点E在线段AB的垂直平分线上.以上结论正确的有( )
 如图,AC=BD,AC⊥BC于C,BD⊥AD于D,AC与BD交于点E.有下列结论:①△ABC≌△BAD;②△ADE≌△BCE;③点E在线段AB的垂直平分线上.以上结论正确的有( )
如图,AC=BD,AC⊥BC于C,BD⊥AD于D,AC与BD交于点E.有下列结论:①△ABC≌△BAD;②△ADE≌△BCE;③点E在线段AB的垂直平分线上.以上结论正确的有( )| A. | ① | B. | ② | C. | ①和② | D. | ①和②和③ |
15.一元二次方程x(x-2)=x-2的根是( )
| A. | 0 | B. | 1 | C. | 1,2 | D. | 0,2 |
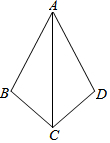 如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC.那么可添加条件为∠BAC=∠DAC.
如图,∠B=∠D,请添加一个条件(不得添加辅助线),使得△ABC≌△ADC.那么可添加条件为∠BAC=∠DAC.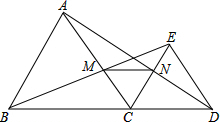 如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.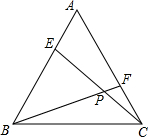 如图,E、F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P.
如图,E、F分别是等边三角形ABC的边AB,AC上的点,且BE=AF,CE、BF交于点P.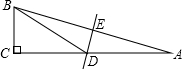 如图,在Rt△ABC中,∠ACB=90°,∠A=15°,AB的垂直平分线与AC交于点D,与AB交于点E,连结BD.若AD=10cm,则BC的长为5cm.
如图,在Rt△ABC中,∠ACB=90°,∠A=15°,AB的垂直平分线与AC交于点D,与AB交于点E,连结BD.若AD=10cm,则BC的长为5cm.