题目内容
五金商店准备从机械厂购进甲、乙两种零件进行销售.若每个甲种零件比每个乙种零件的进价少2元,且买5个甲零件与买4个乙零件费用相同.
(1)求每个甲零件与每个乙零件的进价分别为多少元;
(2)若该五金店本次购进甲种零件的数量比乙种零件的数量的3倍还少5个,且该五金店每个甲种零件的售价为12元,每个乙种零件的售价为15元,要使销售这两种零件的总利润超过371元.问至少购进乙种零件多少个?
(3)在(2)的条件下,若购买两种零件的数量不超过95个,那么该五金店购进甲、乙两种零件有几种方案?请设计出来.
(1)求每个甲零件与每个乙零件的进价分别为多少元;
(2)若该五金店本次购进甲种零件的数量比乙种零件的数量的3倍还少5个,且该五金店每个甲种零件的售价为12元,每个乙种零件的售价为15元,要使销售这两种零件的总利润超过371元.问至少购进乙种零件多少个?
(3)在(2)的条件下,若购买两种零件的数量不超过95个,那么该五金店购进甲、乙两种零件有几种方案?请设计出来.
考点:一元一次不等式的应用,二元一次方程组的应用
专题:
分析:(1)设甲零件进价为x元,乙零件进价为y元,根据每个甲种零件比每个乙种零件的进价少2元,且买5个甲零件与买4个乙零件费用相同,列方程组求解;
(2)设购进乙种零件a个,则购进甲种零件(3a-5)个,根据销售这两种零件的总利润超过371元,列不等式求解;
(3)根据总数量不超过95个,列不等式,求出a的取值范围,然后设计出方案.
(2)设购进乙种零件a个,则购进甲种零件(3a-5)个,根据销售这两种零件的总利润超过371元,列不等式求解;
(3)根据总数量不超过95个,列不等式,求出a的取值范围,然后设计出方案.
解答:解:(1)设甲零件进价为x元,乙零件进价为y元,
由题意得,
,
解得:
,
答:甲零件进价为8元,乙零件进价为10元;
(2)设购进乙种零件a个,则购进甲种零件(3a-5)个.
由题意得:(12-8)(3a-5)+(15-10)a>371,
解得:a>23,
答:至少购进乙种零件24个;
(3)由题意得,3a-5+a≤95,
解得:a≤25,
由(2)得;a>23,
∴共有2种方案.
方案一:购进甲种零件67个,乙种零件24个;
方案二:购进甲种零件70个,乙种零件25个.
由题意得,
|
解得:
|
答:甲零件进价为8元,乙零件进价为10元;
(2)设购进乙种零件a个,则购进甲种零件(3a-5)个.
由题意得:(12-8)(3a-5)+(15-10)a>371,
解得:a>23,
答:至少购进乙种零件24个;
(3)由题意得,3a-5+a≤95,
解得:a≤25,
由(2)得;a>23,
∴共有2种方案.
方案一:购进甲种零件67个,乙种零件24个;
方案二:购进甲种零件70个,乙种零件25个.
点评:本题考查了一元一次不等式的应用,解答本题的关键是读懂题意,设出未知数,找出合适的不等关系,列不等式求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,AB=BC,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结DE、DC、AE并延长AE交CD于F.
如图,在△ABC中,AB=BC,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结DE、DC、AE并延长AE交CD于F. 请你利用如图的直角梯形验证勾股定理,即证明a2+b2=c2.
请你利用如图的直角梯形验证勾股定理,即证明a2+b2=c2.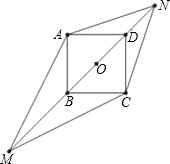 如图,正方形ABCD的边长为1,M,N为BD所在直线上的两点,且
如图,正方形ABCD的边长为1,M,N为BD所在直线上的两点,且