题目内容
18.若$\frac{5x+2}{{x}^{2}-5x+6}$=$\frac{A}{x-2}$+$\frac{B}{x-3}$,则A=-12,B=17.分析 已知等式右边通分并利用同分母分式的加法法则计算,再利用分式相等的条件求出A与B的值即可.
解答 解:∵$\frac{5x+2}{(x-2)(x-3)}$=$\frac{A(x-3)+B(x-2)}{(x-2)(x-3)}$,
∴5x+2=(A+B)x-3A-2B,
即$\left\{\begin{array}{l}{A+B=5}\\{-3A-2B=2}\end{array}\right.$,
解得:A=-12,B=17,
故答案为:-12;17
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
13.若x=2012,则代数式$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$$÷\frac{x-1}{{x}^{2}+x}$的值为( )
| A. | 2010 | B. | 2011 | C. | 2012 | D. | 1 |
10.若分式$\frac{x-4}{x+2}$的值为0,则x的值为( )
| A. | -2 | B. | 4 | C. | -2或4 | D. | 无法确定 |
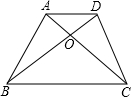 如图,在梯形ABCD中,AD∥BC,AC、BD相交于点O,若S△OAB:S△OBC=1:4,
如图,在梯形ABCD中,AD∥BC,AC、BD相交于点O,若S△OAB:S△OBC=1:4,