Question

6．如图，△ABC中，∠BAC=90°，AB=AC，点D在直线BC上，△ADE是等腰直角三角形，∠DAE=90°，AD=AE，连接CE．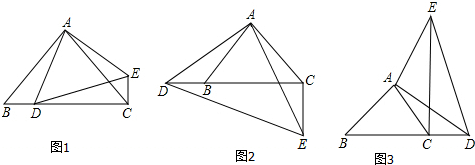

（1）当点D在线段BC上时，如图1，求证：DC+CE=$\sqrt{2}$AC；
（2）当点D在线段CB延长线上时，如图2，求证：$\sqrt{2}$AC=CD-CE
（3）当点D在线段BC延长线上时（如图3），探究线段DC、CE、AC之间的数量关系，并证明．

Answer 1

分析 （1）利用△ABC是等腰直角三角形，易得AB=AC，∠BAC=90°，即有∠BAD+∠DAC=90°，同理可得AD=AE，∠DAC+∠CAE=90°，从而可证∠BAD=∠CAE，从而利用SAS可证△BAD≌△CAE，那么BD=CE，于是BC=CE+DC，再利用勾股定理可知BC=$\sqrt{2}$AC，进而可证CE+DC=$\sqrt{2}$AC；
（2）同（1）可证△BAD≌△CAE，那么BD=CE，而BC+BD=CD，易证$\sqrt{2}$AC=CD-CE；
（3）$\sqrt{2}$AC=CE-CD，同理可证△ACE≌△ABD，得到BD=CE，即BC+CD=CE，所以BC=CE-CD，即证$\sqrt{2}$AC=CE-CD．

解答 解：（1）∵△ABC是等腰直角三角形，
∴AB=AC，∠BAC=90°，
即∠BAD+∠DAC=90°，
同理有AD=AE，∠DAC+∠CAE=90°，
∴∠BAD=∠CAE，
在△BAD和△CAE中，
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$，
∴△BAD≌△CAE，
∴BD=CE，
∴BC=CE+DC，
在Rt△ABC中，BC=$\sqrt{2}$AC，
∴CE+DC=$\sqrt{2}$AC；
（2）∵△ABC是等腰直角三角形，
∴AB=AC，∠BAC=90°，
即∠BAE+∠EAC=90°，
同理有AD=AE，∠DAB+∠BAE=90°，
∴∠BAD=∠CAE，
在△BAD和△CAE中，
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$，
∴△BAD≌△CAE，
∴BD=CE，
又∵BC+BD=CD，
∴BC=CD-CE，
即$\sqrt{2}$AC=CD-CE；
（3）$\sqrt{2}$AC=CE-CD．
在△ACE和△ABD中，
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$，
∴△ACE≌△ABD，
∴BD=CE，
即BC+CD=CE，
∴BC=CE-CD，
∴$\sqrt{2}$AC=CE-CD．

点评 本题考查了等腰直角三角形的性质、全等三角形的判定和性质、勾股定理．解题的关键是利用SAS证明△BAD≌△CAE．