题目内容
9．
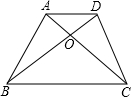如图，在梯形ABCD中，AD∥BC，AC、BD相交于点O，若S△OAB：S△OBC=1：4，则S△OAD：S△OCB=$\frac{1}{16}$．
分析 根据等高三角形的比，可得等高三角形底边的比，根据相似三角形的判定与性质，可得答案．
解答 解：∵S△OAB：S△OBC=1：4
∴OA：OC=1：4．
又AD∥BC
故△OAD∽△OCB
故S△OAD：S△OCB=（$\frac{OA}{OC}$）2=1：16，
故答案为：1：16．
点评 本题考查了相似三角形的判定与性质，利用等高三角形的比得出等高三角形底边的比是解题关键．
练习册系列答案
习题精选系列答案
相关题目
如图，已知△ABC和直线L，作出△ABC关于直线L对称的图形△A′B′C′．
如图的正五角星中，与∠A的2倍互补的角有10个．
19．
如图，已知△ABC与△DEF是全等三角形，则∠B=（ ）
如图，已知△ABC与△DEF是全等三角形，则∠B=（ ）| A． | ∠F | B． | ∠D | C． | ∠DEF | D． | ∠A |