Question

8．已知直角坐标系中有两点A（a，0）和B（b，0），且满足|a-b+5|+$\sqrt{2a+b+1}$=0．
（1）若点C在y轴上，且S_△ABC=10，求点C的坐标；
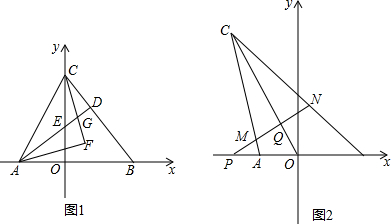
（2）如图1，若点C为y轴正半轴上一点，连接AC，BC，作AD⊥BC于点D，交y轴于点E，CF和AF分别平分∠BCO和∠BAD，求∠AFC的度数；
（3）如图2，若点C在第二象限，且CO平分∠ACB，点P是x轴上点A左侧一动点，PQ⊥OC于点Q，交AC和BC于点M，N，当点P运动时，$\frac{∠BAC-∠ABC}{∠APN}$的值是否发生变化？如果不变，请求出它的值，如果变化，请求出它的范围．

Answer 1

分析 （1）根据|a-b+5|+$\sqrt{2a+b+1}$=0，可以求得a，b的值，从而得到点A，B的坐标，由点C在y轴上，且S_△ABC=10，可以求得点C的坐标．
（2）根据题意可得∠ECD=∠EAH，CF和AF分别平分∠BCO和∠BAD，从而可以求得∠1=∠2=∠3=∠4，从而推出△GCD和△GAF的三个内角分别相等，从而可以求得∠AFC的度数．
（3）过点A作MN的平行线AH交BC于点H，由等腰三角形的知识可以得到△CMN和△CAH都为等腰三角形，再根据三角形的外角等于和它不相邻的两个外角的和，进行灵活变化，从而得到问题的答案．

解答 解：（1）∵|a-b+5|+$\sqrt{2a+b+1}$=0，
∴$\left\{\begin{array}{l}{a-b+5=0}\\{2a+b+1=0}\end{array}\right.$．
解得，$\left\{\begin{array}{l}{a=-2}\\{b=3}\end{array}\right.$．
∴点A的坐标为（-2，0），点B的坐标为（3，0）．
∴线段AB=3-（-2）=5．
又∵点C在y轴上，且S_△ABC=10，
设点C的坐标为（0，y）．
∴$\frac{5×|y|}{2}=10$．
得|y|=4．
∴y=±4．
∴点C的坐标为（0，4）或（0，-4）．
（2）如下图所示：

∵OA⊥OC，
∴∠AOE=90°．
∴∠OAE+∠OEA=90°．
又∵AD⊥BC，
∴∠EDC=90°．
∴∠DEC+∠DCE=90°．
又∵∠OEA=∠DEC，
∴∠OAE=∠DCE．
∵CF和AF分别平分∠BCO和∠BAD，
∴∠1=∠2，∠3=∠4．
∴∠1=∠2=∠3=∠4．
又∵∠2+∠OHA=90°，∠OHA=∠CHF，
∴∠3+∠CHF=90°．
∴∠F=90°．
即∠AFG=90°．
（3）当点P运动时，$\frac{∠BAC-∠ABC}{∠APN}$的值不变．
如下图所示：过点A作MN的平行线AH交BC于点H．

∵CO平分∠ACB，PQ⊥OC于点Q，交AC和BC于点M，N，
∴△CMN为等腰三角形．
∵MN∥AH，
∴∠CNM=∠CHA，∠CMN=∠CAH．
∵∠CNM=∠CMN，
∴∠CHA=∠CAH．
∴△CAHS是等腰三角形．
∴∠BAC=∠BAH+∠HAC=∠BAH+∠CHA．
∴∠BAC-∠ABC=∠BAH+∠CHA-∠ABC．
∵∠CHA=∠BAH+∠ABC，
∴∠BAC-∠ABC=2∠BAH．
∵AH∥MN，
∴∠APN=∠BAH．
∴$\frac{∠BAC-∠ABC}{∠APN}=\frac{2∠BAH}{∠BAH}=2$．

点评 本题考查坐标与图形的性质，三角形的面积，三角形的外角的知识，典型题目|a-b+5|+$\sqrt{2a+b+1}$=0．可知绝对值里面的式子和根号里面的式子都为0．本题的关键是分析好题目中给出的信息，灵活变化，得到解答问题用到的有用信息，最终解答问题．