题目内容
14．已知x2n=5，则（2x3n）2÷4x2n×0.5（xn）2=62.5．分析 原式利用积的乘方与幂的乘方运算法则变形，将已知等式代入计算即可求出值．
解答 解：∵x2n=5，
∴原式=4x6n÷4x2n×0.5x2n=0.5x6n=0.5×125=62.5，
故答案为：62.5
点评 此题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图：在△ABC中，∠C=70°，∠B=30°，AD平分∠BAC，AE⊥BC，垂足为E，求∠DAE的度数．
在△ABC中，AB=AC，AB=13，BC=10，BD⊥AC于D．
如图，在△ABC中，AB=9cm，AC=6cm，D是线段AB的一点，AD=3，点E时线段AC上的任意一点，当AE为多少时，△ADE与△ABC相似？
10．小明为了解同学们的课余生活，设计了如下调查问题：
你平时最喜欢的一项课余活动是（ ）
A．看课外书 B．体育活动 C．看电视 D．踢足球
你认为此问题的答案选项设计合理吗？为什么？如果不合理，请修改．
你平时最喜欢的一项课余活动是（ ）
A．看课外书 B．体育活动 C．看电视 D．踢足球
你认为此问题的答案选项设计合理吗？为什么？如果不合理，请修改．
7．
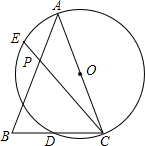如图，在△ABC中，已知AB=AC，∠B=70°，以AC为直径作⊙O交BC于点D，弦CE交AB于点P，且∠ACE=20°，则$\frac{AP}{BC}$的值是（ ）
如图，在△ABC中，已知AB=AC，∠B=70°，以AC为直径作⊙O交BC于点D，弦CE交AB于点P，且∠ACE=20°，则$\frac{AP}{BC}$的值是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{3}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
8．某商场经理接到的采购部和销售部的两个电话，根据电话内容完成下列问题：
（1）写出该商场卖这种商品每天的销售利润y（元）与每件销售价x（元）之间的函数关系式，并指出自变量x的取值范围．
（2）当销售价为多少元时，每天的销售利润最大？最大利润为多少？
（1）写出该商场卖这种商品每天的销售利润y（元）与每件销售价x（元）之间的函数关系式，并指出自变量x的取值范围．
（2）当销售价为多少元时，每天的销售利润最大？最大利润为多少？
| 采购部 | 经理，这里有一批商品以每件42元购回 |
| 销售部 | 经理，以每件42元购回的商品，每天的销售量t（件）与每件的销售价x（元）呈现的关系是：t=-3x+204 |