题目内容
5．
在△ABC中，AB=AC，AB=13，BC=10，BD⊥AC于D．（1）求sinC的值；
（2）求sin∠CBD的值．
分析 （1）作等腰三角形底边上的高AH与BD交点为E，并根据勾股定理求出AH，即可求得sinC的值；
（2）根据同角的余角相等得到∠CBD=∠CAH，然后由等角的三角函数相等得到结论．
解答 解：（1）如图：
过点A作AH⊥BC，垂足为点H，交BD于点E．
∵AB=AC=13，BC=10
∴BH=CH=5
在Rt△ABH中，AH=$\sqrt{A{C}^{2}-C{H}^{2}}$=12，
∴在Rt△EBH中，sin∠C=$\frac{AH}{AC}$=$\frac{12}{13}$；
（2）∵BD⊥AC，
∴∠C+∠CBD=90°，
∵∠C+∠CAH=90°，
∴∠CBD=∠CAH，
∴sin∠CBD=sin∠CAH=$\frac{CH}{AC}$=$\frac{5}{13}$．
点评 此题考查了解直角三角形，等腰三角形的性质，主要利用三角函数的意义，勾股定理来解决问题．
练习册系列答案
相关题目
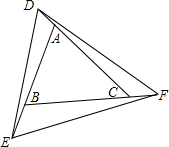如图所示，已知△ABC，延长CA、AB、BC到D、E、F，连接DE、EF、FD，使得∠AED=∠BFE=∠CDF．若∠ABC=60°，∠DFE=50°，求∠BAC及∠EDF的度数．
某长方形广场除四角外都是空地，四角都是一块半径相同的四分之一圆的草坪，若圆形草坪的半径为r，长方形的长为a，宽为b，请用整式表示空地的面积，并指出这个整式是单项式还是多项式．若是单项式，指出它的系数；若是多项式，指出它有几项，各项的系数分别是多少？