题目内容
15.若AD,AE分别是△ABC的中线和角平分线,则下列结论错误的是( )| A. | B、C两点到AE的距离相等 | B. | 点E到AB、AC的距离相等 | ||
| C. | B、C两点到点D的距离相等 | D. | B、C两点到AD的距离相等 |
分析 根据角平分线性质和三角形的中线定义逐个判断即可.
解答 解:A、∵AE是△ABC的角平分线,
∴AE(A除外)上各个点到AB和AC的距离相等,而B、C两点到AE的距离不一定相等,故本选项正确;
B、∵AE是△ABC的角平分线,
∴点E到AB、AC的距离相等,故本选项错误;
C、∵AD是△ABC的中线,
∴BD=DC,故本选项错误;
D、
过B作BF⊥AD于F,过C作CE⊥AD于E,
则∠CED=∠F=90°,
∵AD为△ABC的中线,
∵BD=CD,
在△BFD和△CED中
$\left\{\begin{array}{l}{∠F=∠CED}\\{∠BDF=∠CDE}\\{BD=CD}\end{array}\right.$
∴△BFD≌△CED,
∴BF=CE,
即B、C两点到AD的距离相等,故本选项错误;
故选A.
点评 本题考查了三角形的中线和三角形的角平分线性质的应用,能熟记知识点是解此题的关键,注意:角平分线上的点到这个角的两边的距离相等.

练习册系列答案
相关题目
18. 如图,AB、CD相交于O,OE⊥AB,那么下列结论错误的是( )
如图,AB、CD相交于O,OE⊥AB,那么下列结论错误的是( )
 如图,AB、CD相交于O,OE⊥AB,那么下列结论错误的是( )
如图,AB、CD相交于O,OE⊥AB,那么下列结论错误的是( )| A. | ∠AOC与∠BOD是对顶角 | B. | ∠AOC与∠COE互为余角 | ||
| C. | ∠BOD与∠COE互为余角 | D. | ∠COE与∠BOE互为补角 |
3.函数y=ax2+2(a≠0)的图象经过点(a,10),则a的值为( )
| A. | ±2 | B. | -2 | C. | 2 | D. | 3 |
10.对于实数a,b,c,d规定一种运算:$\left|\begin{array}{cc}a&b\\ c&d\end{array}\right|$=ad-bc,如$\left|\begin{array}{cc}1&0\\ 2&-2\end{array}\right|$=1×0+2×(-2)=-4,那么$\left|\begin{array}{cc}2&-4\\(2-x)&5\end{array}\right|$=25时,x等于( )
| A. | -$\frac{23}{5}$ | B. | $\frac{23}{5}$ | C. | -$\frac{23}{4}$ | D. | -$\frac{13}{4}$ |
20.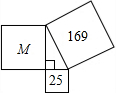 如图,喜羊羊和美羊羊分别做了面积为25和169的两个正方形纸板,村长看到后,把他俩做的正方形和沸羊羊做的正方形M如图放在一起,中间空出的三角形正好是直角三角形,那么正方形M的面积是( )
如图,喜羊羊和美羊羊分别做了面积为25和169的两个正方形纸板,村长看到后,把他俩做的正方形和沸羊羊做的正方形M如图放在一起,中间空出的三角形正好是直角三角形,那么正方形M的面积是( )
 如图,喜羊羊和美羊羊分别做了面积为25和169的两个正方形纸板,村长看到后,把他俩做的正方形和沸羊羊做的正方形M如图放在一起,中间空出的三角形正好是直角三角形,那么正方形M的面积是( )
如图,喜羊羊和美羊羊分别做了面积为25和169的两个正方形纸板,村长看到后,把他俩做的正方形和沸羊羊做的正方形M如图放在一起,中间空出的三角形正好是直角三角形,那么正方形M的面积是( )| A. | 12 | B. | 13 | C. | 144 | D. | 194 |
7.在等腰直角△ABC的斜边AB所在的直线上,有点P满足S=AP2+BP2,则( )
| A. | 对P有无限多个位置,使得S<2CP2 | |
| B. | 对P有有限多个位置,使得S<2CP2 | |
| C. | 当且仅当P为AB的中点,或者P与顶点A,B之一有重合时,才有S=2CP2 | |
| D. | 对直线AB上的所有点P,总有S=2CP2 |
4.若x<-1,则x-$\sqrt{(2-x)^{2}}$-2|x-1|等于( )
| A. | 0 | B. | 4x-4 | C. | 4-4x | D. | 4+4x |