题目内容
18.已知x,y是实数,且(x-y+1)2与$\sqrt{5x-3y-3}$互为相反数,求$\sqrt{{x}^{2}+{y}^{2}}$的值.分析 根据互为相反数的和为零,可得二元一次方程组,根据解方程组,可得x、y的值,根据开方运算,可得答案.
解答 解:由(x-y+1)2与$\sqrt{5x-3y-3}$互为相反数,得
(x-y+1)2+$\sqrt{5x-3y-3}$=0,
$\left\{\begin{array}{l}{x-y+1=0}\\{5x-3y-3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{3}{4}}\\{y=\frac{7}{4}}\end{array}\right.$,
$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{\frac{9}{16}+\frac{49}{16}}$=$\frac{\sqrt{58}}{4}$.
点评 本题考查了二元一次方程组,由互为相反数的和为零得出二元一次方程组是解题关键.

练习册系列答案
相关题目
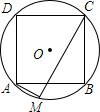 如图,边长为4$\sqrt{2}$的正方形ABCD内接于⊙O,AM是⊙O的内接正十二边形的一边,求CM的长.
如图,边长为4$\sqrt{2}$的正方形ABCD内接于⊙O,AM是⊙O的内接正十二边形的一边,求CM的长.