题目内容
10．在Rt△ABC中，∠C=90°，tanA=$\frac{5}{12}$，周长为30，求△ABC的面积．分析 根据正切函数是对边比邻边，可得a、b的值，根据勾股定理，可得c根据周长公式，可得x的值，根据三角形的面积公式，可得答案．
解答 解：由在Rt△ABC中，∠C=90°，tanA=$\frac{5}{12}$，得
a=5x，b=12x．
由勾股定理，得
c=$\sqrt{{a}^{2}+{b}^{2}}$=13x．
由三角形的周长，得
5x+12x+13x=30，
解得x=1，
a=5，b=12．
S△ABC=$\frac{1}{2}$ab=$\frac{1}{2}$×5×12=30．
点评 本题考查了解直角三角形，利用正切函数表示出a=5x，b=12x是解题关键．
练习册系列答案
相关题目
20．已知|x|=1，|y|=$\frac{1}{2}$，则（x20y）3-（x3y2）2的值为（ ）
| A． | $\frac{1}{16}$或-$\frac{3}{16}$ | B． | -$\frac{1}{16}$或-$\frac{3}{16}$ | C． | $\frac{1}{16}$ | D． | -$\frac{3}{16}$ |
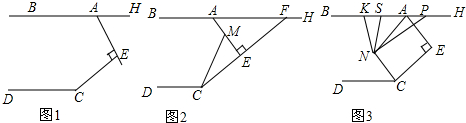
如图，将△ABC纸片折叠，使C落在三角形的内部，求证：∠ADC+∠BEC=2∠C．