题目内容
6.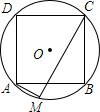 如图,边长为4$\sqrt{2}$的正方形ABCD内接于⊙O,AM是⊙O的内接正十二边形的一边,求CM的长.
如图,边长为4$\sqrt{2}$的正方形ABCD内接于⊙O,AM是⊙O的内接正十二边形的一边,求CM的长.
分析 连接AC、OM,作MH⊥AC于H,根据正方形的性质得到AC是⊙O的直径、求出AC的长,根据直角三角形的性质求出MH=$\frac{1}{2}$OM,根据勾股定理求出答案.
解答 解:连接AC、OM,作MH⊥AC于H,
∵四边形ABCD是正方形,
∴∠D=90°,
∴AC为⊙O的直径,且AC=8,
∵AM是⊙O的内接正十二边形的一边,
∴∠AOM=$\frac{360°}{12}$=30°,
∴MH=$\frac{1}{2}$OM=2,
由勾股定理得,OH=$\sqrt{O{M}^{2}-M{H}^{2}}$=2$\sqrt{3}$,
则CH=4+2$\sqrt{3}$,
∴CM=$\sqrt{C{H}^{2}+M{N}^{2}}$
=$\sqrt{32+16\sqrt{3}}$
=2$\sqrt{6}$+2$\sqrt{2}$.
点评 本题考查的是正多边形和圆的有关计算,掌握正多边形的中心角的求法、直径所对的圆周角是直角和正方形的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.下列分式中,与分式$\frac{3}{x}$相等的是( )
| A. | $\frac{9}{{x}^{2}}$ | B. | $\frac{3x}{{x}^{2}}$ | C. | $\frac{3x}{3{x}^{2}}$ | D. | $\frac{3x}{3x}$ |
 ÷14=-156.
÷14=-156.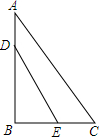 如图,直角三角形ABC中,AB=4,AC=5,BC=3,D、E分别为AB和BC边上的动点,是否存在某一特殊位置使得线段DE既平分△ABC的面积又平分△ABC的周长.
如图,直角三角形ABC中,AB=4,AC=5,BC=3,D、E分别为AB和BC边上的动点,是否存在某一特殊位置使得线段DE既平分△ABC的面积又平分△ABC的周长.