题目内容
6.设a、b、c均为实数,且满足a2+b2+c2=6a+10b+26c-203,化简2$\sqrt{a+\sqrt{b-\sqrt{c+4\sqrt{a}}}}$.分析 根据已知条件写成三个完全平方式的和,根据非负数的性质求得a、b、c的值,再进一步代入化简求值即可.
解答 解:∵a2+b2+c2=6a+10b+26c-203,
∴a2+b2+c2-6a-10b-26c+203=0,
∴(a-3)2+(b-5)2+(c-13)2=0,
∴a-3=0,b-5=0,c-13=0,
∴a=3,b=5,c=13,
∴2$\sqrt{a+\sqrt{b-\sqrt{c+4\sqrt{a}}}}$
=2$\sqrt{3+\sqrt{5-\sqrt{(\sqrt{12}+1)^{2}}}}$
=2$\sqrt{3+\sqrt{4-2\sqrt{3}}}$
=2$\sqrt{3+\sqrt{(\sqrt{3}-1)^{2}}}$
=2$\sqrt{2+\sqrt{3}}$
=$\sqrt{8+4\sqrt{3}}$
=$\sqrt{(\sqrt{6}+\sqrt{2})^{2}}$
=$\sqrt{6}$+$\sqrt{2}$.
点评 此题考查配方法的运用,非负数的性质,二次根式的化简,掌握完全平方公式是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
17.下列分式中,与分式$\frac{3}{x}$相等的是( )
| A. | $\frac{9}{{x}^{2}}$ | B. | $\frac{3x}{{x}^{2}}$ | C. | $\frac{3x}{3{x}^{2}}$ | D. | $\frac{3x}{3x}$ |

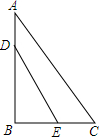 如图,直角三角形ABC中,AB=4,AC=5,BC=3,D、E分别为AB和BC边上的动点,是否存在某一特殊位置使得线段DE既平分△ABC的面积又平分△ABC的周长.
如图,直角三角形ABC中,AB=4,AC=5,BC=3,D、E分别为AB和BC边上的动点,是否存在某一特殊位置使得线段DE既平分△ABC的面积又平分△ABC的周长.